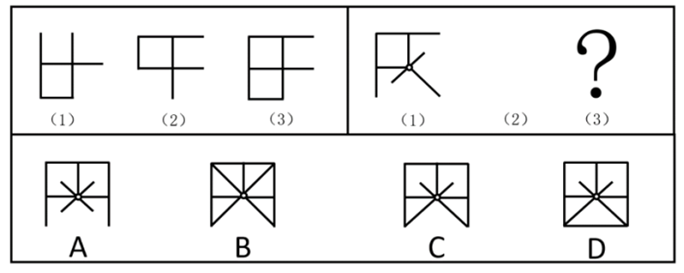
下列两组图形均由(1)(2)(3)三个图形组成,三个图形之间存在一定变化规律。按其规律右边这组图形中,图(3)应为:【2022上海B078】
如图所示
如图所示
如图所示
如图所示
一个半径为120米的圆形人工湖正中有一个半径为60米的圆形人工岛。甲从岛的正北岸边出发,以1米/秒的速度匀速划船前往湖的正南岸边,则最少需要多长时间?
不到3分45秒
3分45秒~4分之间
4分~4分15秒之间
超过4分15秒
(1)不幸死亡
(2)劣质针剂
(3)流通各地
(4)缺乏监管
(5)接种疫苗
3-4-5-1-2
3-1-2-5-4
2-3-5-4-1
4-2-3-5-1
某单位男女员工的人数之比是15:13。按人数之比5:7:8,分为甲、乙、丙三个科室,其中甲科室男女员工的人数之比为4:3,乙科室为5:2。则丙科室男女员工人数之比为:
1:2
2:3
5:9
5:8
甲、乙、丙、丁、戊5名职工参加党史知识测验,每人得分均不相同。甲和乙的平均分比丙多2分,丁和戊的平均分比丁多5分,甲、乙的平均分比丙、丁、戊的平均分多3分。问丙、丁、戊三人得分的排序为:
丙>丁>戊
丙>戊>丁
丁>丙>戊
戊>丙>丁
甲和乙两辆车同时从A地出发匀速开往B地,甲车出发时的速度比乙车快20%,但乙车行驶2小时后速度加快30千米/小时继续匀速行驶,又用了3小时与甲车同时抵达。问A、B两地相距多少千米:
510
540
570
600
甲生产零件的效率比乙高50%,1小时内甲比乙多生产8个零件。现安排甲、乙共同生产1小时,从生产的零件中抽取3件。问至少有1件是甲生产的概率在以下哪个范围内?
小于0.80
0.80~0.90之间
0.90~0.95之间
大于0.95
局长找甲、乙、丙三位处长谈话,计划与甲交谈10分钟,与乙交谈12分钟,与丙交谈8分钟。办公室助理通过合理调整三人交谈的顺序,使得三人交谈和等待的总时间最少。请问调整后的总时间为多少:
46分钟
48分钟
50分钟
56分钟
(1)母亲因伤心过度而发病
(2)报案未果
(3)弟弟夭折
(4)单车寻亲
(5)母亲走失
3-5-1-2-4
5-3-2-4-1
3-1-5-2-4
5-2-4-1-3
(1)旅游井喷
(2)黄金周长假
(3)完善服务
(4)管理失位
(5)景点拥堵
5-1-4-2-3
2-1-4-5-3
2-5-1-3-4
3-2-4-5-1