-27,-7,1,3,5,13,()
33
31
27
25
有一堆围棋子,白子数是黑子的3倍。每次拿出5颗白子、3颗黑子,经过若干次后,剩下的白子数是黑子数的9倍。问原来白子最少有几颗:
22
27
33
66
1/2,3/2,11/8,1,21/32,( )
7/64
25/64
13/32
13/64
1辆汽车原价为20万元,商家促销,预存1000元可拥有1万元抵用券,之后还可以再打9折,则购买这辆汽车总共需支付的金额是:
17.1万元
17.2万元
18.1万元
18.2万元
三位专家为10幅作品投票,每位专家分别都投出了5票,并且每幅作品都有专家投票。如果三位专家都投票的作品列为A等,两位专家投票的作品列为B等,仅有一位专家投票的作品列为C等,则下列说法正确的是:
A等和B等共6幅
B等和C等共7幅
A等最多有5幅
A等比C等少5幅
2014年1—9月我国入境外国游客中,来自亚洲1182.9万人,其中男性785.9万人,女性397.0万人;日本、韩国男性分别为160.5万人、191.3万人,女性分别为38.7万人、116.4万人。来自美洲227.8万人,其中男性142.3万人,女性85.5万人;美国、加拿大男性分别为98.3万人、27.6万人,女性分别为55.7万人、20.9万人。来自欧洲408.7万人,其中男性247.2万人,女性161.5万人;英国、德国、法国、俄罗斯男性分别30.8万人、35.3万人、24.8万人、13.9万人,女性分别为13.4万人,12.7万人、13.0万人、4.4万人。来自大洋洲58.3万人,其中男性35.6万人,女性22.7万人;澳大利亚男性为29.5万人,女性为18.8万人。分年龄段的来自部分国家的入境人数见下表。
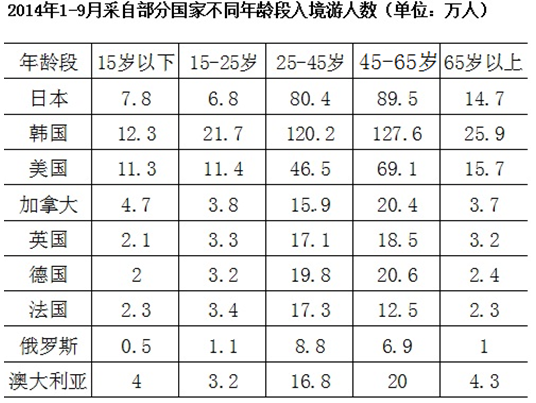
2014年1—9月来自加拿大、英国、法国、俄罗斯的入境游人数由多到少排序正确的是:
加拿大、英国、法国、俄罗斯
英国、加拿大、法国、俄罗斯
加拿大、英国、俄罗斯、法国
英国、加拿大、俄罗斯、法国
日常工作中,如果一件事发展得太过顺利,我们总会隐隐觉得有哪里不对,这样的直觉是有道理的。澳大利亚和法国的研究者们最近在某学术期刊上发表了一篇文章,说明了为什么当所有的证据都指向同一个结果时,它反而可能有问题。他们将此称之为“一致性悖论”。
研究者以证人指认犯人为例研究了一致性悖论,发现在辨认嫌疑人过程中,系统偏差可能来自多种心理偏差,如警方给证人展示照片的方式、证人自身的个人偏见等。而研究者发现,哪怕是细小的偏差都会对最终的整体结果产生极大影响。具体来讲,即使在1%的辨认过程中施加偏差,如暗示某人是犯人,最终当3个以上的证人意见一致时,他们的意见就不再可靠。有趣的是,如果_______,那么其他证人正确的概率反而会大大增加。
为什么会这样?可以用数学中的贝叶斯分析来说明。以扔硬币为例:如果我们有一枚硬币,扔到正面的概率为55%,而非普通硬币的50%,只要扔的次数足够多,就会发现正面向上多于反面向上的次数,进而发现这个硬币是有问题的。换句话说,当我们看到投掷结果中正面向上的次数显著多于反面向上时,就会意识到出问题的是硬币,而非概率定理。同样,根据概率定理,很多证人同时得到一致结论的可能性极低,所以更有可能的是系统出了差错。
在警方组织的嫌疑人指认中,指认同一个人有罪的证人数目越多,这个人真正有罪的概率就越大。然而,这只适用于没有任何系统偏差存在的理想情况。实际情况中,当指认同一个人为犯人的证人数目增加到一个值以后,该嫌疑人真正有罪的概率反而会下降,最终与随机指认毫无差别,且系统偏差越大,概率下降得越早。比方说,如果你让证人完成一项较为容易的任务,比如从一堆香蕉中找出一个苹果,所有人都几乎不会出错,多人结论一致的情况就可能出现,而指认犯人要比在一堆香蕉中找到苹果复杂得多。模拟显示,如果_______,他们认错人的概率会高达48%,在这种情况下,许多证人同时指认一个人为犯人的概率就相当低了;但如果_______,他们认错人的概率会大大降低,多个证人结论一致的情况出现的可能性也会提高。
在法律领域之外,一致性悖论还有很多用武之地,一个重要的应用就是加密技术。数据加密通常通过确认一个很大的数字是否为质数来进行,这个判断过程的错误率要达到非常低才行:低于2的负128次方才可以接受。在这一过程中,可能出现的系统差错就是计算机故障。大多数人都不会想到宇宙射线会导致电脑将一个合数误认为质数,毕竟这件事发生的概率只有10的负13次方——但要注意,这个概率要大于我们所要求的误差(2的负128次方),所以这类误差主导了整个过程的安全性。正因于此,加密协议所宣称的安全程度越高,实际的过程就越容易受计算机故障影响。
一致性悖论虽然听起来违背直觉,但研究者解释,一旦我们了解了足够的信息,就能理解它了。
根据本文,一致性悖论产生的根本原因在于:
过程复杂
系统偏差
主观因素影响
评价标准不唯一
日常工作中,如果一件事发展得太过顺利,我们总会隐隐觉得有哪里不对,这样的直觉是有道理的。澳大利亚和法国的研究者们最近在某学术期刊上发表了一篇文章,说明了为什么当所有的证据都指向同一个结果时,它反而可能有问题。他们将此称之为“一致性悖论”。
研究者以证人指认犯人为例研究了一致性悖论,发现在辨认嫌疑人过程中,系统偏差可能来自多种心理偏差,如警方给证人展示照片的方式、证人自身的个人偏见等。而研究者发现,哪怕是细小的偏差都会对最终的整体结果产生极大影响。具体来讲,即使在1%的辨认过程中施加偏差,如暗示某人是犯人,最终当3个以上的证人意见一致时,他们的意见就不再可靠。有趣的是,如果_______,那么其他证人正确的概率反而会大大增加。
为什么会这样?可以用数学中的贝叶斯分析来说明。以扔硬币为例:如果我们有一枚硬币,扔到正面的概率为55%,而非普通硬币的50%,只要扔的次数足够多,就会发现正面向上多于反面向上的次数,进而发现这个硬币是有问题的。换句话说,当我们看到投掷结果中正面向上的次数显著多于反面向上时,就会意识到出问题的是硬币,而非概率定理。同样,根据概率定理,很多证人同时得到一致结论的可能性极低,所以更有可能的是系统出了差错。
在警方组织的嫌疑人指认中,指认同一个人有罪的证人数目越多,这个人真正有罪的概率就越大。然而,这只适用于没有任何系统偏差存在的理想情况。实际情况中,当指认同一个人为犯人的证人数目增加到一个值以后,该嫌疑人真正有罪的概率反而会下降,最终与随机指认毫无差别,且系统偏差越大,概率下降得越早。比方说,如果你让证人完成一项较为容易的任务,比如从一堆香蕉中找出一个苹果,所有人都几乎不会出错,多人结论一致的情况就可能出现,而指认犯人要比在一堆香蕉中找到苹果复杂得多。模拟显示,如果_______,他们认错人的概率会高达48%,在这种情况下,许多证人同时指认一个人为犯人的概率就相当低了;但如果_______,他们认错人的概率会大大降低,多个证人结论一致的情况出现的可能性也会提高。
在法律领域之外,一致性悖论还有很多用武之地,一个重要的应用就是加密技术。数据加密通常通过确认一个很大的数字是否为质数来进行,这个判断过程的错误率要达到非常低才行:低于2的负128次方才可以接受。在这一过程中,可能出现的系统差错就是计算机故障。大多数人都不会想到宇宙射线会导致电脑将一个合数误认为质数,毕竟这件事发生的概率只有10的负13次方——但要注意,这个概率要大于我们所要求的误差(2的负128次方),所以这类误差主导了整个过程的安全性。正因于此,加密协议所宣称的安全程度越高,实际的过程就越容易受计算机故障影响。
一致性悖论虽然听起来违背直觉,但研究者解释,一旦我们了解了足够的信息,就能理解它了。
根据本文,下列哪种情况中可能存在一致性悖论:
检测站对某公司生产的所有新车及使用5年以上的旧车分别进行了尾气检测,检测结果为该公司生产的新车均达到尾气排放标准
低空跳伞世界级选手辛普森有2000次高空跳伞和1400次低空跳伞的经历,但是,他的第1401次低空跳伞,因降落伞未打开而以失败告终
两个城市的两位彩民凭借机选票分享一等奖两注,这两张在同一分钟购买的彩票,不仅中大奖那注号码一致,没中奖的两注机选号码也完全一致
在欧洲殖民者发现澳大利亚的黑天鹅之前,欧洲人曾经认为天鹅都是白色的,后来欧洲人登陆澳大利亚后,一上岸竟发现有黑色的天鹅
日常工作中,如果一件事发展得太过顺利,我们总会隐隐觉得有哪里不对,这样的直觉是有道理的。澳大利亚和法国的研究者们最近在某学术期刊上发表了一篇文章,说明了为什么当所有的证据都指向同一个结果时,它反而可能有问题。他们将此称之为“一致性悖论”。
研究者以证人指认犯人为例研究了一致性悖论,发现在辨认嫌疑人过程中,系统偏差可能来自多种心理偏差,如警方给证人展示照片的方式、证人自身的个人偏见等。而研究者发现,哪怕是细小的偏差都会对最终的整体结果产生极大影响。具体来讲,即使在1%的辨认过程中施加偏差,如暗示某人是犯人,最终当3个以上的证人意见一致时,他们的意见就不再可靠。有趣的是,如果_______,那么其他证人正确的概率反而会大大增加。
为什么会这样?可以用数学中的贝叶斯分析来说明。以扔硬币为例:如果我们有一枚硬币,扔到正面的概率为55%,而非普通硬币的50%,只要扔的次数足够多,就会发现正面向上多于反面向上的次数,进而发现这个硬币是有问题的。换句话说,当我们看到投掷结果中正面向上的次数显著多于反面向上时,就会意识到出问题的是硬币,而非概率定理。同样,根据概率定理,很多证人同时得到一致结论的可能性极低,所以更有可能的是系统出了差错。
在警方组织的嫌疑人指认中,指认同一个人有罪的证人数目越多,这个人真正有罪的概率就越大。然而,这只适用于没有任何系统偏差存在的理想情况。实际情况中,当指认同一个人为犯人的证人数目增加到一个值以后,该嫌疑人真正有罪的概率反而会下降,最终与随机指认毫无差别,且系统偏差越大,概率下降得越早。比方说,如果你让证人完成一项较为容易的任务,比如从一堆香蕉中找出一个苹果,所有人都几乎不会出错,多人结论一致的情况就可能出现,而指认犯人要比在一堆香蕉中找到苹果复杂得多。模拟显示,如果_______,他们认错人的概率会高达48%,在这种情况下,许多证人同时指认一个人为犯人的概率就相当低了;但如果_______,他们认错人的概率会大大降低,多个证人结论一致的情况出现的可能性也会提高。
在法律领域之外,一致性悖论还有很多用武之地,一个重要的应用就是加密技术。数据加密通常通过确认一个很大的数字是否为质数来进行,这个判断过程的错误率要达到非常低才行:低于2的负128次方才可以接受。在这一过程中,可能出现的系统差错就是计算机故障。大多数人都不会想到宇宙射线会导致电脑将一个合数误认为质数,毕竟这件事发生的概率只有10的负13次方——但要注意,这个概率要大于我们所要求的误差(2的负128次方),所以这类误差主导了整个过程的安全性。正因于此,加密协议所宣称的安全程度越高,实际的过程就越容易受计算机故障影响。
一致性悖论虽然听起来违背直觉,但研究者解释,一旦我们了解了足够的信息,就能理解它了。
第5段中“正因于此”的“此”,指的是:
加密技术判断过程的错误率并不可能达到2的负128次方
除宇宙射线外,还有其他因素会引起计算机的系统误差
上述加密技术的判断过程是在目前使用最为广泛的方法
出现计算机故障的概率高于加密技术判断过程的错误率
1,3,6,11,18,( )
25
27
29
33