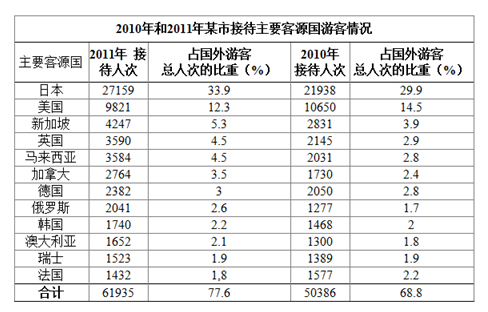
若2012年加拿大、韩国、法国到该市旅游人次与2011年保持相同的增长速度,DC、Dk、Df 分别表示2012年该市接待这三个国家游客人次占接待主要客源国游客总人次的比重,则下列正确的是:
DC>Dk>Df
Df>DC>Dk
Df<DC<Dk
DC<Df<Dk
朋友见面打招呼,过去是“吃饭了吗”,如今流行“搬新家了吗”“旅游了吗”“进修了吗”。这种现象可以反映出:
恩格尔系数时小时大
恩格尔系数变小
恩格尔系数不变
恩格尔系数变大
华光高科技公司在进行人才招聘时,有小张、小李、小王、小赵、小钱等5人入围。
从学历看,这5人中有2人为硕士,3人为博士;
从年龄看,这5人中有3人小于30岁,2人大于30岁。
已知,小张、小王属于相同的年龄段,而小赵、小钱属于不同的年龄段;
小李与小钱的学位相同,小王和小赵的学位不同。
最后,只有一位年龄大于30岁的硕士应聘成功。
据此,可以推出应聘成功者是:
小张
小王
小赵
小钱
某条道路安装了60盏功率相同的路灯,如将其中24盏的灯泡换为200瓦的节能灯泡,则所有路灯的耗电量将比之前节约20%。如将所有灯的灯泡换为150瓦的节能灯泡,则耗电量能比之前节约多少?
62.5%
50%
75%
64%
2014年6月23日,《食品安全法(修订草案)》将_______十二届全国人大常委会第九次会议审议。国家食药监管总局官员介绍,“重典治乱”成为本次修法的主导思想,将设立最严格的程序_______法律制度,建立最严格的法律责任制度,大幅提高企业违法成本,政府失职将被_______。
填入横线部分最恰当的一项是:
递交 监视 训责
提交 监管 问责
提交 监管 谴责
交付 监督 审问
甲、乙两个圆柱体容器的底面积之比为2:3,容器中的水深分别为10厘米和5厘米。先将甲容器中的水倒一半在乙容器中,则此时两个容器中的水深之比为:
3:5
3:4
2:3
2:5
某电影公司准备在1~10月中选择两个不同的月份,在其当月的首日分别上映两部电影。为了避免档期冲突影响票房,现决定两部电影中间相隔至少3个月,则有( )种不同的排法。
21
28
42
56
中国是一个古代典籍十分丰富的国家,中华民族自古就是一个爱书、读书的民族。尽管因为各种天灾人祸,历代典籍遗留至今的十不存一,但据不完全统计,我国现存古籍仍有约19万种,其中保存在公共图书馆系统的就有2750万册,可列入善本的约有250万册。在长期的藏书、聚书活动中,古代读书人养成了鉴书、校书的传统,如西汉河间献王刘德从民间征购藏书,必留献书人的正本,且只收先秦古文字写成的旧籍;宋人欧阳修读书,闻人有善本者,必求而改正之。值得一提的是,不同历史时期的人们对书籍的选择形成了近乎相同的标准,即都把目光投向了善本。
根据这段文字,接下来最可能讲的是:
鉴书和校书传统对当代文化的影响
古代文人书籍选择标准的形成过程
善本在当代文化研究与传播中的作用
善本的具体概念及其文化、学术价值
有3个单位共订300份《人民日报》,每个单位最少订99份,最多101份。问一共有多少种不同的订法:
4
5
6
7
一个没有理想的人将_______地度过一生,一个没有理想的国家将是一盘散沙;一个没有理想的人必定注重眼前的_______,一个没有理想的国家就会变成少数人捞取私利的工具。多年的改革开放已经冲破了旧有意识形态的束缚,人民的认知水平有了极大的提高,现在是重树理想的时候了。
依次填入划横线处最恰当的一项是:
浑浑噩噩 功过得失
糊里糊涂 小恩小惠
得过且过 功名利禄
碌碌无为 蝇头小利