某市举行“新春杯”足球比赛，对16支参赛队伍进行小组赛分组抽签。抽签箱中分别装有红、黄、绿、蓝的小球各四个，抽到相同颜色小球的队伍进入同一小组。则第一支抽签队伍与第二支抽签队伍被分在同一小组的概率为（）。
二分之一
三分之一
四分之一
五分之一
已知一种液体的密度随深度而增大，它的变化规律是ρ=ρ0+kh，式中ρ0、k是常数，h表示深度。设深度足够，有一个密度ρ′的实心小球投入此液体中，且ρ′＞ρ，则小球的运动过程表述正确的是：（本题只考虑小球受到重力和浮力两个力）
小球会经历若干次加速和匀速过程，最后沉底
小球一直加速，最后沉底
小球会经历若干次匀速和减速过程，最后悬浮在液体中某处
小球会经历若干次加速和减速过程，最后悬浮在液体中某处
中秋节前夕，小赵买了6个外观相同的月饼，其中有3个是蛋黄馅的。回到家后，小赵从中任取3个月饼，里面恰好有1个是蛋黄馅的概率是：
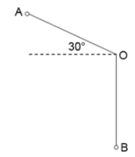
长为1米的细绳上系有一个小球，从A处放手以后，小球第一次摆到最低点B处共移动了多少米：
有甲、乙、丙三个轻质小球，已知甲与乙相互吸引，甲与丙相互排斥，则以下说法正确的是：
若乙带正电，丙可能带正电
若乙带正电，丙可能不带电
若丙带负电，乙可能带负电
若丙带负电，乙可能不带电
某市场调查公司3个调查组共40余人，每组都有10余人且人数各不相同。2017年重新调整分组时发现，若想分为4个人数相同的小组，至少需要新招1人；若想分为5个人数相同的小组，至少还需要新招2人。问原来3个组中人数最多的组比人数最少的组至少多几人？
2
3
4
5
设n为正整数，如果存在一个完全平方数（比如，5×5=25，25就是一个完全平方数），使得在十进制表示下此完全平方数的各数字之和为n，那么n被称作好数（比如，7是一个好数，因为25的各数字之和为7）。那么，在1，2，3，……，2017中共有（ ）个好数？
895
896
897
898
899
900
901
902
一个布袋中装有大小相同的3个白球、4个红球和2个黑球，每次从袋中摸出一球不再放回。问恰好在第3次取得黑球的概率是多少？
某村过年有分肉的习俗。将160斤肉分给村里的110户家庭，贫困家庭每户分得3斤肉，其他家庭每户分得1斤肉。那么该村的贫困家庭有多少户：
16
20
22
25
现有3个箱子，依次放入1、2、3个球，然后将3个箱子随机编号为甲、乙、丙，接着在甲、乙、丙3个箱子里分别放入其箱内球数的2、3、4倍。两次共放了22个球。最终甲箱中的球比乙箱：
多1个
少1个
多2个
少2个
。
，
。
。
米。
。
。
。
。
，化解的A-C=2。