[单选题]

某单位在边长为200米的正方形广场上组织一场招聘会，计划安排若干名工作人员提供咨询服务，每名工作人员入场后将分别随机站在一个位置上，其服务半经不超过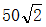米。若要确保咨询服务全覆盖，则至少需要安排工作人员：

A . 4名
B . 5名
C . 6名
D . 7名

参考答案： A

参考解析：

①分析覆盖需求与圆的特性：
正方形广场边长为200米，每个工作人员的服务半径为米（直径为米≈141.42米）。需用最少的圆（服务范围）覆盖整个正方形区域。

②分割正方形与圆的覆盖范围：
将边长200米的正方形分割为4个边长100米的小正方形，每个小正方形的对角线长度为1002米（与服务圆的直径相等）。
每个小正方形的中心作为服务圆的圆心，圆心坐标可设为(50,50)、(150,50)、(50,150)、(150,150)（以大正方形左下角为原点(0,0)）。
每个服务圆的半径为米，恰好覆盖对应小正方形的所有顶点（顶点到圆心的距离为米，等于半径），且小正方形内任意点到圆心的距离均≤半径（例如边中点到圆心的距离为50米＜米）。

③验证全覆盖：
4个服务圆分别覆盖4个小正方形，且在大正方形中心（100,100）及四条边中点处均被相邻圆覆盖，无遗漏区域。
因此，至少需要4名工作人员。

故本题选A。
【2025-江苏B-062】