[单选题]

在边长为2正方形中投入若干石子(石子大小忽略不计)，问至少投几个石子才能使这些石子中一定存在距离不超过的两个石子？

A . 5
B . 6
C . 7
D . 8

参考答案： A

参考解析：

①画图分析：
为了“一定存在距离不超过的两个石子”，即离得尽可能远的石子之间仍存在距离不超过的石子，
如图所示，先在正方形中相距最远的A、B、C、D四个点各投放一个石子，共4个石子；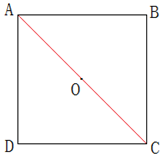

连接对角线AC（即正方形内最远距离），此时距四个顶点最远的那个点为O点，向O点投一个石子。

②算出答案：
由于正方形边长为2，可得，则，满足距离不超过的要求，则共至少投5个石子。

故本题选A。
【2023-山东-039】

视频解析：