[单选题]

某公司职员小王要乘坐公司班车上班，班车到站点的时间为上午7点到8点之间，班车接人后立刻开走；小王到站点的时间为上午6点半至7点半之间。假设班车和小王到站的概率是相等（均匀分布）的，那么小王能够坐上班车的概率为：

A .
B .
C .
D .

参考答案： D

参考解析：

方法一：
①分析题意：
正面考虑比较复杂，可以通过反面考虑。小王能够坐上班车的概率=1-小王不能坐上班车的概率；
由于人能等车，但车不会等人，故小王在6:30~7:00到站或班车在7:30~8:00到站时，一定能够坐上车；
因此小王不能坐上车的情况为，小王和班车均在7:00~7:30时间内到站，且班车比小王早；
根据题意，班车和小王到站的概率是相等（均匀分布）的，则小王在7:00~7:30到达的概率为，班车在7:00~7:30到达的概率为，班车比小王早的概率也为；

②算出答案：
则小王不能坐上班车的概率为，则小王能够坐上班车的概率=。

方法二：
①建立坐标系：
因为时间是连续的，故可以在直角坐标系中绘制图形根据面积来计算概率，如下图所示：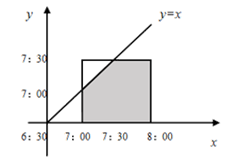

横轴x为班车到站点时间，纵轴y为小王到站点时间；
其中，正方形是按照各自的时间到达的总面积，阴影部分为小王能够坐上班车的部分（y<x，即小王到站点的时间早于班车）。

②算出答案：
设正方形边长为1，则面积=1×1=1；
白色部分面积=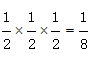，则阴影部分面积=。
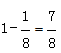所求概率=。

故本题选D。
【2021-联考/山西-063】

视频解析：