[单选题]

某公司职员预约某快递员上午9点30分到10点在公司大楼前取件，假设两人均在这段时间内到达，且在这段时间到达的概率相等。约定先到者等后到者10分钟，过时交易取消。快递员取件成功的概率为：

A .
B .
C .
D .

参考答案： C

参考解析：

方法一：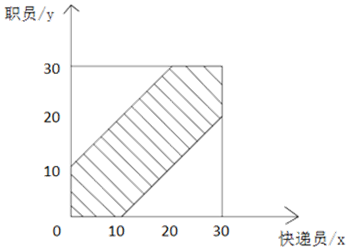

①画出函数图像：
设快递员x分钟到达公司大楼，职员y分钟到达公司大楼，则只有两人到达时间不超过10分钟，即x-y≤10或y-x≤10时，才能完成交易；
9：30到10：00之间有30分钟，由题意可得x，y的取值范围为0≤x≤30，0≤y≤30，则x-y≤10、y-x≤10、0≤x≤30、0≤y≤30所围成的区域即上图阴影部分区域两人才能够相遇，交点坐标分别为（0，10）、（20，30）、（30，30）、（30，20）、（10，0）、（0，0）；
快递员取件成功的概率即阴影部分面积在整个正方形面积的占比。

②算出答案：
由图可以看出，正方形面积为30×30=900，空白部分为两个全等三角形，面积为（30-10）×（30-10）÷2×2=20×20=400，则阴影部分面积为900-400=500，占总面积的500÷900=。

方法二：
①列出所有情况：
由于他们到达概率相等，则第一个人在9:30～9:40到达的概率为，第二个人在9:40～9:50到达的概率也为，相遇概率为；
第一个人在9:40～9:50到达的概率为，第二个人在9:50～10:00到达的概率也为，相遇概率为；
第一个人在9:50～10:00到达的概率为，由于均在9:30～10:00这段时间到达，则第二个人在9:50～10:00到达的概率为1，相遇概率为；

②算出答案：
分类相加，则他们相遇的概率为。

故本题选C。
【2020-联考/湖北-067】

视频解析：