[单选题]

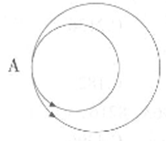
某儿童娱乐场有两条圆形赛车跑道，大圆跑道直径80米，小圆跑道直径60米，两跑道于发车起点A处相切重合。假设甲、乙两辆车同时从A点以相同速度出发（甲跑大圈、乙跑小圈），且此后速度均保持不变。则第一次相距最远时，甲、乙各跑了（）圈。

A . 2，3
B .
C . 3，2
D .

参考答案： B

参考解析：

方法一：
由“甲、乙两辆车同时从A点以相同速度出发”可知，甲车与乙车走过的总路程是相同的。又因为总路程=周长×圈数，则周长与圈数成反比。
大、小圆跑道周长之比为直径之比=80∶60=4∶3；则甲车乙车圈数比=3：4。
观察选项，只有B选项符合。

方法二：
当甲跑至A点相对面，乙跑至A点时相距最远为80米，
此时甲跑的是整数圈加半圈，可排除A、C选项；乙跑的是整数圈；
大圈周长80π，小圈周长60π；
甲乙同时以相同速度出发，时间相同，则行驶路程应相等：
B选项：甲行驶距离==乙行驶距离=60π×2，当选。
D选项：甲行驶距离=≠乙行驶距离=60π×2，排除；

故本题选B。
【2015-深圳-052】

视频解析：