[单选题]

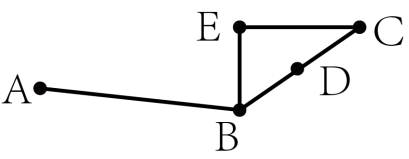
人行步道ABC如图所示，BC两地之间的距离为286米，D地为BC中点，AD两点间的直线距离为324米。现经B点作直线BE，从C点作垂直于BE的直线CE并与BE相交于E点。问EA之间的最短距离为多少米？

A . 38
B . 168
C . 176
D . 181

参考答案： D

参考解析：

①算出ED：
过B点作直线BE有无数条，所以从C点作垂直于BE的直线CE也有无数条，因此E点为以D点为圆心，ED为变径的圆上任意点；
由于D为BC中点，且∠E为90°，根据直角三角形斜边中线定理：
ED=BD=CD= =143米。

②由三角形的两边之和大于第三边可知：
EA+ED＞AD，可得EA＞AD-ED=324-143=181米,观察选项没有符合。
但当E、D、A三点在一条直线时，EA=AE-ED=181米。

故本题选D。
【2019-黑龙江公检法-064】

视频解析：