[单选题]

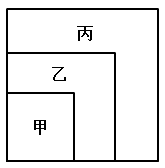
在一个正方形内画中、小两个正方形，使三个正方形具有公共顶点，这样大正方形被分割成了正方形区域甲和L形区域乙、丙。已知三块区域甲、乙、丙的周长之比为4：5：7，并且区域丙的面积为48，求大正方形的面积：

A . 96
B . 98
C . 200
D . 102

参考答案： B

参考解析：

第一步：判断题型------本题为几何问题

第二步：分析作答：
通过平移可以看出，甲、乙、丙的周长就是大、中、小三个正方形的周长；
由于正方形的面积比=周长比的平方，故三个正方形的面积比为16：25：49。
设三个正方形的面积分别为16x，25x和49x，则，解得x=2；
所以大正方形的面积为49×2=98。

故本题选B。
【2012-深圳-049】