[单选题]

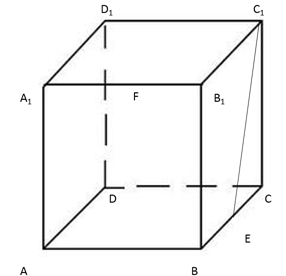
如下图所示，一个边长为10厘米的正方体木块ABCD-A1B1C1D1，点E、F分别是BC、A1B1的中点，C1E是用蜂蜜画的一条线段，一只蚂蚁在点F处，要想沿正方体表面最快到达蜂蜜所在线段C1E，它所爬行的最短距离是多少厘米：

A .
B .
C .
D .

参考答案： B

参考解析：

①画图表示：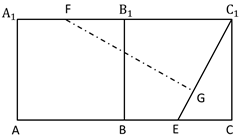

将正方体的两个面ABB1A1、BCC1B1展开，得到矩形ACC1A1，如图所示。

②算出长度：
EC=5厘米，CC1=10厘米，厘米。

③算出答案：
在面ACC1A1中，过点F作FG⊥EC1。
∠FGC1=∠C1CE=90°，∠EC1F+∠C1FG=∠EC1F+∠EC1C=90°。
因此∠C1FG=∠EC1C，则△FC1G∽△EC1G。
所以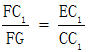，FC1=10+5=15厘米，即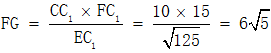厘米。

故本题选B。
注：本题最短距离存在争议，蚂蚁沿着A1B1C1D1表面，从F直接爬到C1，则爬行的最短距离=FC1=，但选项没有此答案，故依然按照最短距离计算出答案为B。
【2017-联考/黑龙江-071】

视频解析：