[单选题]

甲、乙等36人分为6个小组参加某项活动，要求任意2组人数不同，每个组都不少于3人，且任何一组人数不得超过另一组的3倍。问甲和乙至少有1人分到人数第二多的小组的概率为：

A . 25%
B . 30%
C . 35%
D . 40%

参考答案： D

参考解析：

①分析题意确定六小组的人数：
“任意2组人数各不同，每个组都不少于3人”，可先给最小的组分3人，则6个组人数从小到大依次为：3、4、5、6、7、8，此时已分完3+4+5+6+7+8=33人，
又“任何一组人数不得超过另一组的3倍”，剩余3人只能分别分在人数较多的三个组，所以六个组人数依次为：3、4、5、7、8、9人，第二多的小组人数为8人。

②考虑最不利情况数：
该组选人的总情况数36人中选8人，则有种情况；
甲乙都没有进入该组，从其他34人中选择8人，有种情况。

③算出答案：
则所求概率为1-甲乙不在8人组的概率=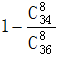=40%。

故本题选D。
【2024-国考副省级-069】

视频解析：