[单选题]

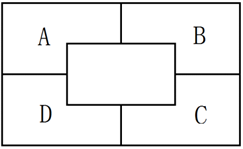
如图所示，一面墙被分成A、B、C、D四块，现有4种不同的颜色，要求在每一块里涂上一种颜色且相邻的两块颜色不相同(可以使用少于4种颜色)，问有几种不同的涂法？

A . 84
B . 64
C . 36
D . 24

参考答案： A

参考解析：

①算出涂A、B的情况：
先涂A，从4个颜色选1个，有4种情况；
再涂B，由于AB相邻，则AB不同色，从剩余3个颜色中选1个，有3种情况；

②算出涂C、D的情况：
由于C与A是否同色，影响着D颜色的选择，分类讨论：
1）若C、A同色，C只有1种选择；D与A不同色，从剩下的3种颜色中选1个，有3种情况；共1×3=3种情况。
2）若C、A不同色，且C与B不同色，则从剩下2种颜色中选1个，有2种情况；D与A、C不同色，从剩下2种颜色选1个，共2种情况；共2×2=4种情况；
分类相加，共3+4=7种情况；

③算出答案：
总情况数共4×3×7=84种情况。

故本题选A。
【2023-四川-055】

视频解析：