[单选题]

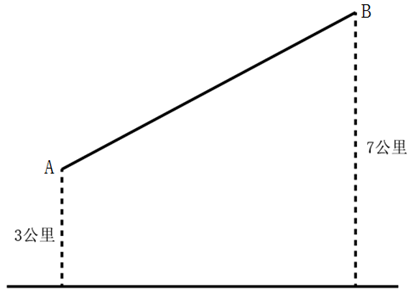
A、B两村在一条笔直公路的同侧，到公路的垂直距离分别是3公里和7公里，两村相距8.5公里，现需在公路边建一个物资集散中心，为节约物资配送成本，集散中心到两个村的直线路程之和应尽可能小，若货车的速度约为60公里/小时，那么货车从集散中心出发，到两村送货后返回中心，路途所花费的最少时间为：

A . 18分钟
B . 21分钟
C . 24分钟
D . 27分钟

参考答案： B

参考解析：

①做辅助线，找到最短距离：
如下图，过公路作A点的对称点A´，交公路于点E；
连接A´B，交ED于点O，O即为集散中心，此时集散中心O到两个村的直线路程之和最小，则A´B是到两个村的最小直线路程。
过B点作公路的垂线，垂点为D，延长BD交平行于公路的A´C´于C´；
则A´C´⊥BC´，过A作AC⊥BC，则四边形ACC´A´为矩形。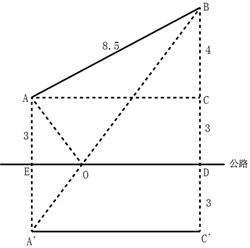


②算出最短路程：
已知AE=3，BD=7，则BC=4；已知AB=8.5，
在△ABC中，AC==7.5，则A´C´=7.5；
BC´=BD+AE=7+3=10；
则在△A´BC´中，=12.5；
货车的速度约为60公里/小时，到两村送货后返回中心，最短距离为OA+AB+BO=A´B+AB=12.5+8.5=21公里；

③算出答案：
需要的最少时间=21÷60×60=21分钟。

故本题选B。
【2023-联考/湖北-062】

视频解析：