[单选题]

12个人排成1列纵队，从前到后编为1～12号。现要将他们排成另一个与原来不同的纵队并从前到后重新编号，要求每个人的新号码与原始号码相差不超过1。那么有多少种重新编队的方法？

A . 155
B . 227
C . 232
D . 239

参考答案： C

参考解析：

①枚举找规律：
将12个人编为1～12号，根据“要求每个人的新号码与原始号码相差不超过1”，即每个人号码数不变，或者只与相邻的人交换号码。
要求与原来不同，则至少应有一组相邻的人交换号码，由于12人情况较多，可以从1人至12人编队依次枚举，并归纳规律得出答案，具体情况如下。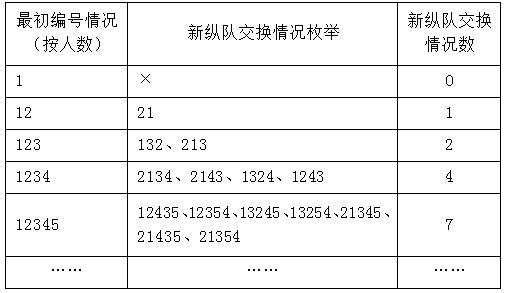


②运用规律，算出答案：
从表格得知，纵队每增加1人，新纵队交换情况数的规律为第三项=前两项和+1，
则依次为0、1、2、4、7、12、20、33、54、88、143、232，
即12人的纵队重新编队后不与原纵队的顺序完全一致的情况数为232种。

故本题选C。
【2023-浙江A-070/浙江B-050/浙江C-050】

视频解析：