[单选题]

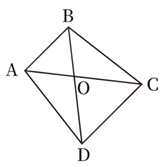
公园里有一片四边形草坪，沿对角线修建的小道相交于0点，O到四个顶点A、B、C、D的距离之比正好为1∶2∶3∶4，一名工人花费1天正好完成AOB区域的修剪，问第二天至少需要额外增加多少名效率相同的工人一起工作，才能在当天内完成剩余草坪的修剪？

A . 8
B . 10
C . 11
D . 12

参考答案： B

参考解析：

①算出四个区域的面积：
赋。因为与的高相同，底边BO：DO=2：4=1：2，
根据“两个三角形的高相同，面积之比等于底之比”，可得；
同理，与的高相同，底边AO：CO=1：3，则；与的高相同，底边AO：CO=1：3，则。

②算出答案：
故剩余草坪面积为=3+6+2=11。
根据“一名工人花费1天正好完成AOB区域的修剪”，即一名工人花费1天修剪的面积为1，则要在第二天完成剩余草坪的修剪至少需要11÷1=11名效率相同的工人，故至少需要额外增加11-1=10名效率相同的工人一起工作。

故本题选B。
【2023-国考行政执法-065/国考市地-065】

视频解析：