[单选题]

A、B两地分别与某个半径150米的圆形池塘边缘相距100米、且AB的连线经过池塘的圆心，张某从A地出发以1米/秒的速度匀速行走。全程除转向1次外均保持直线行进。问他从A地到B地的最短用时在以下哪个范围内？

A . 不到9分30秒
B . 9分30秒～10分之间
C . 10分～10分30秒之间
D . 10分30秒以上

参考答案： C

参考解析：

①算出AD：
如图所示，张某需从A地绕过池塘（圆O），通过外部路径到达B地。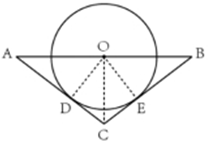

过A点作圆的切线AD，过B点作圆的切线BE，延长AD、BE交于C点，AC＋BC为最短路径。
OD⊥AC，OE⊥BC，且OD=OE，OA=OB，所以，，△ABC为等腰三角形。
AO＝100+150=250米，OD为半径150米，则

②算出最短距离：
因△AOD与△ACO均为直角三角形且∠A为公共角，所以△AOD∽△ACO，
可得，，AC+BC=312.5×2=625米，

③算出最短用时：
需用时625÷1=625秒＝10分25秒，在10分～10分30秒之间。

故本题选C。
【2022-重庆选调-051】

视频解析：