[单选题]

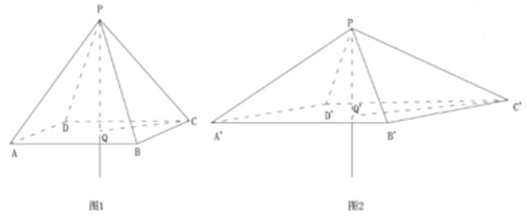
商家门口摆放了一把正四棱锥形（底面为正方形，侧面为四个全等的等腰三角形）的遮阳伞，第一次伞撑开到图1所示的位置，伞柄与伞骨成角∠CPQ为30°，继续撑开到如图2所示的位置，伞柄与伞骨成角变为60°，那么第二次伞撑开后形成的正方形是第一次撑开后正方形ABCD面积的：

A . 倍
B . 倍
C . 2倍
D . 3倍

参考答案： D

参考解析：

①算出两个底面正方形边长之比：
如图所示，连接CQ。
在直角三角形CPQ中，设PC为a，由∠CPQ为30°，得CQ为；
同理，连接C′Q′，C′P为a，由∠C′PQ′为60°，则C′Q′为；
两个正方形边长之比等于对角线的一半之比，即，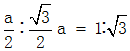

②算出两个底面正方形面积之比：
两个正方形面积之比为边长的平方比，即1:3，则第二个正方形面积是第一个的3倍。

故本题选D。
【2022-联考/陕西-100】

视频解析：