[单选题]

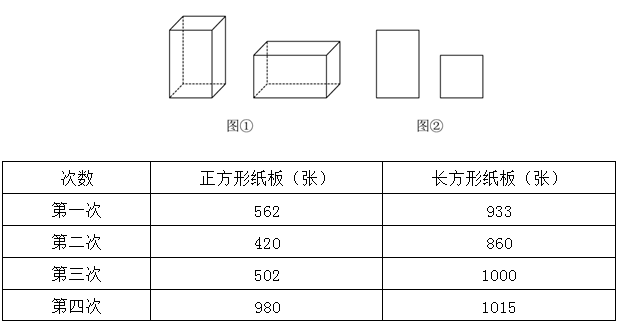
某工厂要做如图①所示的竖式和横式的两种无盖纸盒若干个，需从仓库领取如图②中的长方形和正方形纸板作侧面和底面，每次领取的纸板必须用完。工作人员领取记录如下表，仓库管理员在核查工作人员四次领取纸板数的记录时发现有一次记录有误。问第几次记录有误：

A . 一
B . 二
C . 三
D . 四

参考答案： D

参考解析：

①找到领取的纸板数与制作纸盒个数的关系：
由图①可得，制作左边无盖长方体纸盒需4个长方形和1个正方形，制作无盖右边长方体纸盒需3个长方形和2个正方形。
设制作图①左、右长方体纸盒的个数分别为x、y个。
根据“每次领取的纸板必须用完”，可列式：
x+2y=领取正方形纸板数      ①，
4x+3y=领取长方形纸板数    ②，
两式相加可得：5x+5y=5（x+y）=领取正方形纸板数+领取长方形纸板数；

②验证数据，得到结论：
因为x、y一定是正整数，所以（领取正方形纸板数+领取长方形纸板数）一定是5的整数倍，即尾数是0或5。
用尾数法，第三次领取纸板之和尾数为2，不满足5的整数倍，所以第三次记录有误。
但本题数据存在问题，验证第四次数据，x+2y=980，4x+3y=1015，解得x=-182，y=581，x、y应均为正整数，第四次不符合实际，所以第四次记录也有误。

综上，第三、四次记录都有误，单选题C或D。
【2022-湖南-064】

视频解析：