[单选题]

7名防疫人员负责甲、乙两个社区的居民排查工作，已知每人走访一户居民的用时为固定值，若5人负责甲社区、2人负责乙社区，则完成乙社区排查的时间比甲社区要晚5天；若3人负责甲社区、4人负责乙社区，则乙社区完成排查后，只需6人共同工作4天就能完成甲社区的排查。那么如果要在6天内完成两个社区的排查工作，至少需要额外增加多少人？

A . 5
B . 6
C . 7
D . 8

参考答案： B

参考解析：

根据“每人走访一户居民的用时为固定值”，即每人每天走访居民数也是固定的，赋每名防疫人员每天走访1户居民。
方法一：
①列方程求社区居民数：
设甲社区有x户居民，乙社区有y户居民，可列方程组：
，解得x=45，y=28；

②算出在6天内完成两个社区的排查，至少需要增加人数：
，人数取整，取13人，至少再增加13-7=6人。

方法二：
①列方程求社区居民数：
设第一次排查甲社区需要t天，乙社区需要t+5天，则甲社区工作量为5t，乙社区工作量为2(t+5)。
由于第二次乙社区有2人增加到4人，根据工作总量不变，人数和时间成反比，则第二次排查所需时间变为原来的一半，即，可列式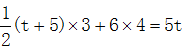，解得t=9，得到甲社区工作量为5×9=45，乙社区工作量为2×(9+5)=28。

②算出在6天内完成两个社区的排查，至少需要增加人数：
，人数取整，取13人，至少再增加13-7=6人。

故本题选B。
【2022-联考/河南-065】

视频解析：