[单选题]

为了实现营养的合理搭配，某营养师拟推出适合不同人群的甲、乙两个品种的饮食。其中，1份甲品种中有3千克A食物、1千克B食物、1千克C食物；1份乙品种中有1千克A食物、2千克B食物、2千克C食物。甲、乙两个品种的成本价分别为A、B、C三种食物的成本价之和。已知A食物每千克的成本价为6元。甲品种每份售价为58.5元，利润为成本的30%，乙品种的利润为成本的20%。问如果两品种的总销售利润率至少要达到总成本的24%，销售甲、乙两个品种饮食的份数之比不应低于多少？

A . 5:7
B . 6:8
C . 7:9
D . 8:9

参考答案： D

参考解析：

①算出甲乙单成本比：
设1千克B食物成本为x元，1千克C食物成本为y元；
甲售价58.5元，利润为成本的30%，可得甲成本元；
甲成本=3×6+x+y=45，化简后x+y=27；
乙成本为6+2x+2y=6+2×（x+y）=60元。
甲乙单成本之比为45:60=3:4。

②算出甲乙总成本比：
由于甲利润率为30%，乙利润里为20%，总利润率至少为24%，根据十字交叉法，可得：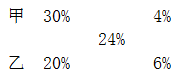

得到甲乙总成本之比为4%:6%=2:3，由于总成本=单成本×份数。

③算出答案：
则甲乙份数之比至少为,即销售甲、乙两个品种饮食的份数之比不应低于8:9。

故本题选D。
【2020-新疆-063】

视频解析：