[单选题]

甲、乙两条生产线每小时分别可以生产15000件和9000件某种零件，产品合格率分别为99%和99.8%。现接到36万件这种零件的生产任务，要求合格率不得低于99.5%，则两条生产线合作，至少需要多少小时完成？

A . 15
B . 18
C . 24
D . 25

参考答案： D

参考解析：

①算出甲乙各自完成生产任务的用时：
设甲完成x件，则乙完成(36-x)件。
合格率=合格零件/生产件数，根据十字交叉法。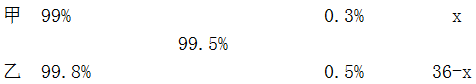

解得x=13.5，即甲完成13.5万件，需用时13.5万÷1.5万=9小时；
乙完成36-13.5=22.5万件，需用时22.5万÷0.9万=25小时。

②得出答案：
由于甲的合格率偏低，若甲完成后帮助乙会导致整体合格率偏低，不符合题意。
故至少需要25小时完成。

故本题选D。
【2022-北京-080/北京延庆-080】

视频解析：