[单选题]

在周长为300米的环形跑道的某处，甲、乙两人分别以6米/秒，3米/秒的速度同时同向出发，沿跑道奔跑，甲每次追上乙后都减速0.5米/秒，直至他们两人的速度相同，问在他们出发后的30分钟内，甲和乙以相同速度跑过的路程为多少米？

A . 990
B . 1080
C . 1530
D . 1800

参考答案： A

参考解析：

方法一：
①算出每次追及时间：
根据题干，环形跑道上从同一点同时出发同向而行，所以每追上一次则甲比乙多跑一圈（300米）。
根据追及公式，S差=V差×t；甲每次追上乙后速度都减少0.5米/秒；

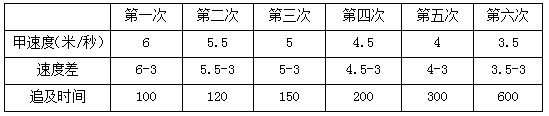
②算出速度不同总时间：
然后甲的速度减少为3.5-0.5=3米/秒，此时两人速度相等，共用时100+120+150+200+300+600=1470秒。

③算出相同速度时间：
30分钟=30×60=1800秒；
则两人同速跑过的时间=1800-1470=330秒。

④算出相同速度路程：
则相同速度跑过的路程=330×3=990米。

方法二：
乙两人初始速度差为6-3=3米/秒，可假设甲的初始速度为3米/秒，乙的初始速度为0，方便计算。其余方法同上。

故本题选A。
【2021-四川-048】