[单选题]

甲、乙、丙从长360米的圆形跑道上的不同点同时出发，沿顺时针方向匀速跑步。3分钟后甲追上乙，又过1分30秒后丙也追上乙，又过3分30秒后丙追上甲，又过5分30秒后丙第二次追上乙。问出发时甲在乙身后多少米？

A . 48
B . 84
C . 108
D . 144

参考答案： B

参考解析：

①画出图形：
甲乙丙的出发点如下图所示。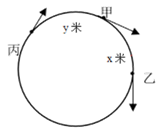

甲丙都追乙，可设乙的速度为0，即乙保持不动。

②算出丙速度：
依据“又过3分30秒后丙追上甲，又过5分30秒后丙第二次追上乙”可知，3.5+5.5=9分钟丙比乙多跑一圈，一圈长度为360米；
根据追及公式，可知V丙=360÷9=40米/分钟；

③算出甲速度：
依据“又过1分30秒后丙也追上乙，又过3分30秒后丙追上甲”可知，甲走1.5+3.5=5分钟的路程，丙只需要走3.5分钟；
根据路程一定，速度和时间成反比，可知V甲：V丙=t丙：t甲=3.5:5=7:10，则V甲=40×=28米/分钟；

④算出答案：
甲追上乙用时3分钟，则出发时甲在乙后3×28=84米。

故本题选B。
【2021-浙江A-071/浙江B-041】

视频解析：