[单选题]

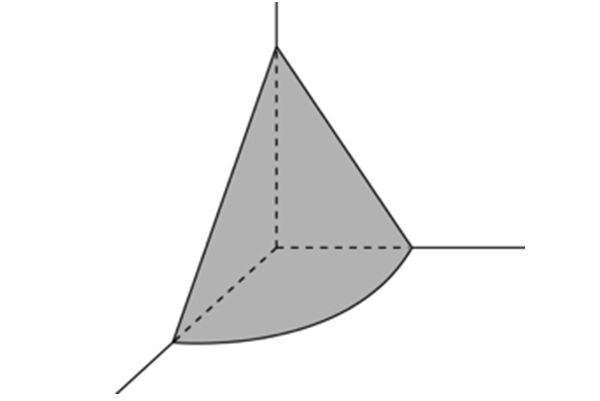
在屋内墙角处堆放稻谷（如图，谷堆为一个圆锥的四分之一），谷堆底部的弧长为6米，高为2米，经过一夜发现谷堆在重力作用下底部的弧长变为8米，若谷堆的谷量不变，那么此时谷堆的高为：

A . 米
B . 米
C . 米
D . 米

参考答案： A

参考解析：

①算出变化前后底面积之比：
谷堆为一个圆锥的四分之一，则底面弧长是底面圆周长的四分之一。根据圆周长公式C=2πr，变化前后圆锥半径之比等于弧长之比=6：8=3：4；底面积之比等于半径之比的平方=3²:4²=9：16；

②算出变化前后高之比：
谷堆的谷量不变，即体积不变。根据圆锥体积公式V=（底面积×高）÷3，高与底面积成反比，即变化前后谷堆的高之比为16：9。

③算出答案：变化前谷堆高为2米，变化后谷堆高为米。

故本题选A。
【2020-联考/山西-041】

视频解析：