[单选题]
有2张1×1的正方形红纸,3张1×1的正方形黄纸,2张1×2的长方形绿纸,所有的纸均颜色均匀。现在将这些纸全部不重叠地贴到一张3×3的正方形白纸上,要求最后的图案为轴对称图形。问总共能贴出多少种满足要求的图案(旋转后重合的图案视为同一种)?
A . 11
B . 10
C . 5
D . 4
参考答案: B
参考解析:
题干要求轴对称图形,可分别进行考虑。
①两个长方形关于正方形对角线对称且相邻,共2种。
先贴两个1×2的长方形绿纸,关与正方形对角线对称且相邻,再贴两个1×1的正方形红纸关于对角线对称,黄纸贴在剩余空白处。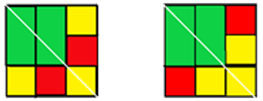
②两个长方形关于正方形对角线对称但不相邻,共4种。
先贴两个1×2的长方形绿纸,关于正方形对角线对称但不相邻,再贴两个1×1的正方形红纸关于对角线对称,黄纸贴在剩余空白处。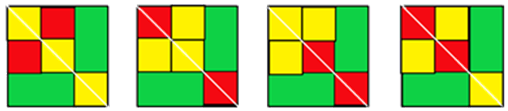
③两个长方形关于正方形横轴或竖轴对称。
因为旋转后重合的图案视为同一种,此处只考虑竖轴一种情况,共4种。先贴两个1×2的长方形绿纸关于竖轴对称,再贴两个1×1的正方形红纸关于竖轴对称,黄纸贴在剩余空白处。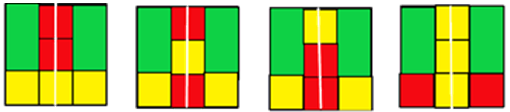
共有2+4+4=10种情况满足要求。
故本题选B。
【2020-山东-044】
视频解析:



