[单选题]

如图，由四个全等的直角三角形拼成一个大正方形，每个三角形的面积都是1，且两直角边之比大于等于2，则这个大正方形的面积至少是：

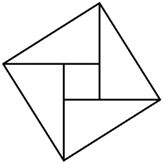
A . 4
B . 5
C . 6
D . 7

参考答案： B

参考解析：

方法一：
①分析题意：
已知大正方形面积=小正方形面积+4×三角形面积=小正方形面积+4。

②算出答案：
观察图形，小正方形面积不可能为2，即小正方形面积不可能为三角形面积的2倍，则答案只能为5。

 方法二：
①分析题意：
已知大正方形面积=小正方形面积+4×三角形面积=小正方形面积+4。

②算出小正方形面积：
设三角形的长直角边为x，短直角边为y，
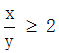则小正方形面积=，由于，因此当x=2y时，小正方形面积最小。
故：x=2y；。
解得x=2，y=1。
故小正方形面积为=1。

③算出答案：因此大正方形的面积为至少为1+4=5。

故本题选B。
【2019-上海B-073】

视频解析：