[单选题]

将一根绳子任意分成三段，则此三段能构成一个三角形的概率是：

A .
B .
C .
D .

参考答案： A

参考解析：

①分析题意，画图表示：
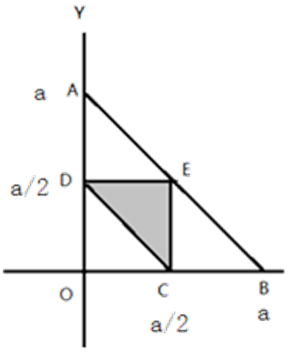
设绳子长为a，三段分别为x、y、a-x-y，且0<x<a，0<y<a，0<a-x-y<a（即0<x+y<a），则根据这三个约束条件可画出取值区间如下图△OAB所示，（其中AB线段表示0<x+y<a）。
  

②算出答案：
要构成一个三角形，则需满足两边之和大于第三边，因此可列下式：
x+y＞a-x-y；x+a-x-y＞y；y+a-x-y＞x。
即：x+y＞；y＜；x＜。
取值区间即为图中阴影部分△CDE。
因此所求概率为灰色△CDE面积占△OAB面积的比值，为。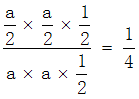

故本题选A。
【2019-江苏A-064】

视频解析：