[单选题]
如图，两个同心圆构成的圆环被均匀地分割成7份，连同中间的小圆共8个区域。若要给这8个区域着色，至少需要（ ）种颜色，才能使相邻区域颜色不同？
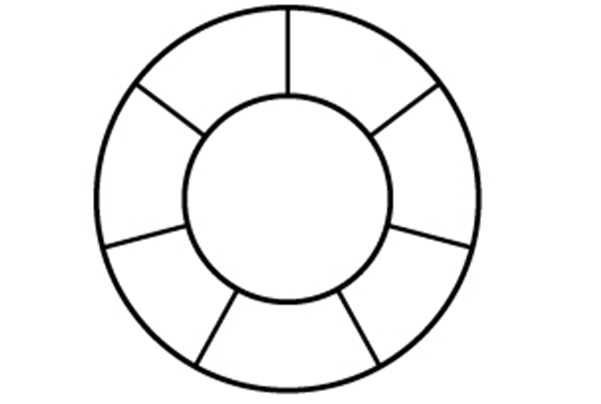
A . 3
B . 4
C . 5
D . 6
参考答案： B
参考解析：
①分析题意：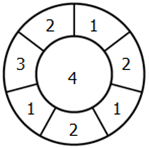
要使相邻区域颜色不同，则小圆与其他区域都相邻，需要1种颜色。
其他区域，按（1、2）为周期涂色，会剩余1个区域，则此时外面区域需要3种颜色。
②算出答案：所以总共需要颜色数=1+3=4种。
故本题选B。
【2018-上海B-074】
视频解析：
答题
解析：