[单选题]
某市规划建设的4个小区，分别位于直角梯形ABCD的4个顶点处（如图），AD=4千米，CD=BC=12千米。欲在CD上选一点S建幼儿园，使其与4个小区的直线距离之和为最小，则S与C的距离是：
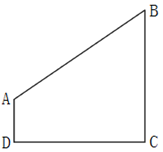
A . 3千米
B . 4千米
C . 6千米
D . 9千米
参考答案： D
参考解析：
①画图表示：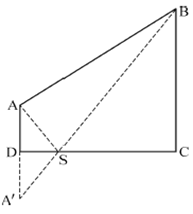
由于在CD上选一点建幼儿园，故S到C、D两点间距离和不变（为CD长），只需满足AS+BS最小即可。过CD作A点的镜像点A'，连接A'B交CD于S，如图所示。
②算出答案：
AS+BS最小，即A'S+BS最小。
AD∥BC，则△A'DS∽△BCS。
则
，即
，已知AD=4，CD=BC=12，解得CS=9。
故本题选D。
【2017-江苏A-069】
视频解析：
答题
解析：