[单选题]

甲乙两人分别从A地、B地同时出发晨练，甲从A地骑车到B地，乙从B地跑步到A地。甲乙在离B地480米时相遇，休息2分钟后又同时继续前行，到达终点后均休息5分钟后返回。当他们第二次相遇时，甲距A地240米，如果骑车和跑步均为匀速运动，且骑车速度大于跑步速度，则甲骑车速度与乙跑步速度之比为：

A . 4：3
B . 3：2
C . 2：1
D . 5：2

参考答案： B

参考解析：

①分析第一次相遇的情况：
甲乙两人第一次相遇时，乙跑了480米，此时甲乙两人共同走过的路程为AB两地间的距离，设为S。
从开始到第一次相遇，甲乙两人运动时间相同，根据时间=路程÷速度，设甲骑车速度为v甲，乙跑步速度为v乙，则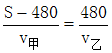                               
，整理可得。

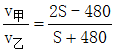②分析第二次相遇的情况：
从开始到第二次相遇，甲乙两人一共走了3个AB两地间的距离，即3S。
因为甲乙两人中途休息时间相同（都休息2+5=7分钟），且运动时间相同，那么他们的路程比等于速度比。
此时甲走过的路程为2S-240米，乙走过的路程为S+240米，所以。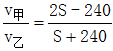

③建立等式求解S：，解得S=1200米。

④计算甲乙速度之比：
把S=1200代入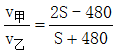，可得甲骑车速度与乙跑步速度之比为3：2。

故本题选B。
【2023-重庆选调-057】

视频解析：