[单选题]

某工业园区内一区域如下图所示，三角形ABC与ACD为两个面积相等的直角三角形，AB长度是BC的2倍。现在区域内划出如图两个圆形区域摆放花坛，两个圆形均与图中两条边相切。已知B点到大圆、D点到小圆上任一点的最短距离分别为AD长度的、，问大圆面积是小圆的多少倍？

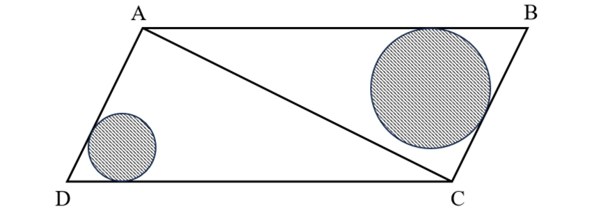
A . 3倍以下
B . 3~3.5倍之间
C . 3.5~4倍之间
D . 4倍以上

参考答案： D

参考解析：

①分析题意画辅助线：
由题意，赋值AB=DC=20，AD=BC=10。
假设大圆圆心为O，AB与大圆相切于点M，连接MO、BO，设BO与大圆交于点N。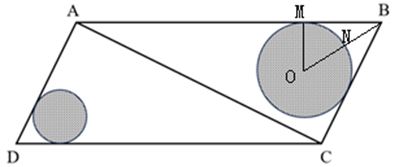


②求大小圆半径：
BN为B到大圆的最短距离，为AD的一半，即为5。
在直角三角形ACB中，BC是AB的一半，由此可知∠BAC=30°，
则∠ABC=60°，∠MBO=30°，
因为AB为大圆切线，M为切点，所以三角形OMB为直角三角形，
根据直角三角形中，30度角所对边等于斜边一半，得到2MO＝BO，
设大圆半径为R，则2R＝R＋5，则R为5。同理可得，小圆半径为2，

③算出答案：
大圆面积∶小圆面积=（5×5）÷（2×2）=25÷4=6.25倍。

故本题选D。
【2025-天津-015】

视频解析：