[单选题]

某巡逻艇在海域A点发现正南方30千米处的B点有一艘可疑船只正匀速向正西方行驶，巡逻艇以比该可疑船只快的速度沿某一方向直线追击，两船恰好在C点相遇。问B、C两点之间的距离约为多少千米？

A . 26
B . 28
C . 30
D . 34

参考答案： D

参考解析：

①根据题意画图：
A点为巡逻艇的位置，B点为可疑船只，在C点被追上。
B点在A点正南方，C点在B点正西方，所以三角形ABC为直角三角形。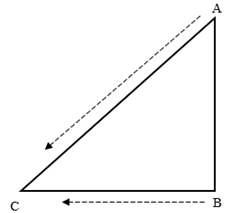


②求出BC距离：
根据“巡逻艇的速度比可疑船快”，赋值，可疑船只的速度为3，则巡逻艇的速度为4，两船的速度比为。
两船在C点相遇，时间相同，路程与速度成正比，可设BC的距离为3s，AC的距离为4s。
根据勾股定理，可得，解得s=。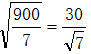
则BC=3s=＞30，只有D选项符合。

故本题选D。
【2024-山东-060】

视频解析：