[单选题]

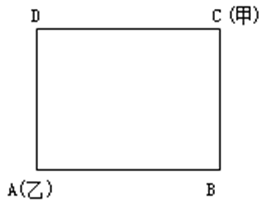
某校园围墙外的道路形成一个边长为300米的正方形(如图所示),甲、乙两人分别从正方形的两个对角沿逆时针方向同时出发，甲、乙的步行速度比为9:7。问甲、乙两人第一次处于同一条边是在哪一条边上？

A . AB
B . BC
C . CD
D . DA

参考答案： D

参考解析：

①根据题意赋值：
根据“甲、乙的步行速度比为9：7”，设甲的速度为9v，则乙的速度为7v。

②分析距离：
甲乙最开始距离为AB+BC=300+300=600米，
到达甲乙两人第一次处于同一条边的时候，两人路程差≤300米。
当甲与乙相差300米时：300=（9v-7v）×t，解得vt=150，则此时甲所走路程=9v×t=1350米（走完一圈300×4=1200米多150米），甲在CD中点，
此时乙所走路程=7v×t=1050米（还差150米走完一圈），乙在DA中点。

③得出答案：
又因为甲速度大于乙速度，当甲到达D点时，乙未到达A点，此时甲、乙两人均在DA边，且为第一次处于同一条边。

故本题选D。
【2024-联考/贵州-055】

视频解析：