[单选题]

正方形水池ABCD的边长为80米。E点在AB边正中的正北30米处，F点在C点东偏南45°方向，F点到C点距离为米。甲从E点出发前往F点，问他的最短行进距离比途经D点的最短行进距离短多少米？

A . 30
B . 50
C .
D . 80

参考答案： D

参考解析：

①算出最短行进距离：
由于ABCD为池塘，无法穿过，且两点之间直线最短，则从E出发前往F的最短行进距离为EB+BF。

②算出途径D点的最短行进距离：
途径D点，需要先从E点到D点，最短距离为EA+AD，再从D点到F点，最短距离为DF，故从E点出发途径D点的最短行进距离为EA+AD+DF。

③算出答案：
如图所示，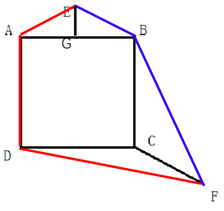

G为AB中点，则AG=BG，∠AGE=∠BGE=90°，EG为公共边，则△AGE≌△BGE，AE=BE；
BC=CD，∠BCF=∠DCF，CF为公共边，则△BCF≌△DCF，BF=DF；
则两种行进距离相差（EA+AD+DF）-（EB+BF）=AD=80米。

故本题选D。
【2024-四川-055】

视频解析：