[单选题]

某学校的运动场是椭圆形。边界椭圆上一点到中心距离的最小值是20米，两点间距离的最大值为80米。若学生在该运动场上排成方阵，则所排成方阵面积的最大值为：

A . 1280平方米
B . 1360平方米
C . 1440平方米
D . 1600平方米

参考答案： D

参考解析：

①写出方阵面积表达式：
根据题意，O为椭圆中心点，如图所示，过O点作x轴、y轴，则a=80÷2=40米，b=20米。
在运动场内排成方阵，若要使方阵面积最大，则需要方阵顶点与椭圆相接。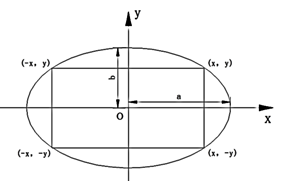

设右上角顶点坐标为（x，y）。
根据对称性，则其余顶点坐标分别为（-x，y）、（x，-y）、（-x，-y），则方阵的长和宽分别为2x、2y米，则方阵面积为2x×2y=4xy平方米。

②算出答案：
根据椭圆标准方程，可列式，即，整理得。
根据不等式a2+b2≥2ab，可得到，则4xy≤1600，即方阵面积的最大值为1600平方米。

故本题选D。
【2023-江苏A-055/江苏B-055】

视频解析：