[单选题]
把一个正方形的四个角分别切除一个等腰三角形，剩下一个长宽不等的矩形。若被切除部分的总面积为400平方厘米，且切除的三角形的直角边的长度均为整数，则所剩矩形的面积为多少平方厘米：
A . 320
B . 336
C . 360
D . 384
E . 400
F . 420
G . 441
H . 464
参考答案： D
参考解析：
①算出总面积方程：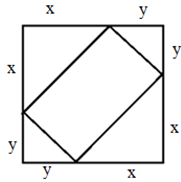
如图，设等腰三角形的腰分别为x厘米、y厘米，
切除部分的总面积为
=
（x，y为整数）；
②算出原正方形边长：
由勾股定理，方程可写成
，解得x=16，y=12。
原正方形边长为x+y=16+12=28厘米；
③算出所剩矩形面积：
等于原正方形面积-400=28×28-400=784-400=384平方厘米。
故本题选D。
【2015-陕西-067】
视频解析：
答题
解析：