甲、乙两汽车分别从P、Q两地同时出发相向而行，途中各自速度保持不变。他们第一次相遇在距P点16千米处，然后各自前行，分别到达Q、P两地后立即折返，第二次相遇在距P点32千米处，则甲、乙速度之比为：
2：3
2：5
4：3
4：5
甲、乙、丙、丁四人同时同地出发，绕一椭圆形环湖栈道行走。甲顺时针行走，其余三人逆时针行走。已知乙的行走速度为60米/分钟，丙的速度为48米/分钟。甲在出发6、7、8分钟时分别与乙、丙、丁三人相遇，求丁的行走速度是多少?
31米/分钟
36米/分钟
39米/分钟
42米/分钟
2020年12月，德尔黑和三位同事在《当代生物学》上发表了文章，他们认为葛洛格将温度和湿度混为一谈了。潮湿的环境使植物生长茂盛，这为动物躲避捕食者提供了荫蔽。因此，动物在潮湿的地方往往颜色更深，以伪装自己。德尔黑说，许多温暖的地方是潮湿的，但潮湿又凉爽的森林也是有的，比如塔斯马尼亚的森林，那里也有最黑的鸟类。
从这段文字可推断出：
德尔黑的观点，动物的颜色在温度低的地方会是浅色的
葛洛格的观点，温暖而潮湿的地区，鸟的羽毛颜色会是深色的
葛洛格的观点，阳光充足的赤道地区，鸟的羽毛颜色会是深色的
德尔黑的观点，阳光充足的赤道地区，鸟的羽毛颜色会是浅色的
如果每500米远架一根电线杆，则30公里需要架设多少根电线杆：
31
30
61
60
甲和乙同时出发，在长360米的环形道路上沿同一方向各自匀速散步。甲出发2圈后第一次追上乙，又走了4圈半第二次追上乙。则甲出发后走了多少米第一次到达乙的出发点？
160
200
240
280
某工厂先从边长为1米的正方形铁皮切割掉一个半径1米、圆心角为直角的扇形，再用剩余材料切割正方形。为充分利用原材料，希望所得正方形越大越好。若不考虑切割损耗，问所切最大的正方形边长约为多少厘米？
22.6
25.6
27.6
31.6
悟空与二郎神在离地面1米的空中决斗，两人相距2米，悟空想用分身直接偷袭二郎神，为了不引起对方的警觉，分身必须在地面反弹一次再进行攻击，则分身到达二郎神的位置所走的最短距离为：
米
米
米
米
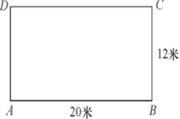
如图，在长方形跑道上，甲、乙两人分别从A、C处同时出发，按顺时针方向沿跑道匀速奔跑，已知甲、乙两人的速度分别是5米/秒、4.5米/秒。则当甲第一次追上乙时，甲沿长方形跑道跑过的圈数是：
4
4.5
5
5.5
甲、乙两人从环形跑道的A点同时出发背向而行，6分钟后两人第一次相遇，相遇后两人的速度各增加10米每分钟，5分钟后两人第二次相遇。问环形跑道的长度为多少米？
600
500
400
300
将一块三角形绿地沿一条直线分成两个区域，一为三角形，一为梯形，已知分出的三角行区域的面积为1.2亩，梯形区域的上、下底边分别为80米、240米，问分出的梯形区域的面积为多少亩：
9.6
11.2
10.8
12.0
千米；
米/分钟。
，乙的速度为
，出发时甲乙相距为S；
，甲比乙多走的距离为环形跑道的长度360米；
，解得S=160。
厘米；
）厘米；
=100（
）÷
≈28.6厘米，因为边长最大约为28.6，不可能再比28.6大，结合选项，最大选27.6。
。
米。
；根据路程相同，速度比等于时间的反比，得
；