圆柱形容器底部放有一个长方体铁块。打开水龙头开始往容器中注水,6分钟水面恰好淹没铁块,再过16分钟灌满容器。若容器和铁块的高分别为45厘米和15厘米,则铁块和容器的体积之比是:
1:12
1:9
1:6
1:3
甲、乙两汽车分别从P、Q两地同时出发相向而行,途中各自速度保持不变。他们第一次相遇在距P点16千米处,然后各自前行,分别到达Q、P两地后立即折返,第二次相遇在距P点32千米处,则甲、乙速度之比为:
2:3
2:5
4:3
4:5
甲、乙、丙、丁四人同时同地出发,绕一椭圆形环湖栈道行走。甲顺时针行走,其余三人逆时针行走。已知乙的行走速度为60米/分钟,丙的速度为48米/分钟。甲在出发6、7、8分钟时分别与乙、丙、丁三人相遇,求丁的行走速度是多少?
31米/分钟
36米/分钟
39米/分钟
42米/分钟
甲和乙同时出发,在长360米的环形道路上沿同一方向各自匀速散步。甲出发2圈后第一次追上乙,又走了4圈半第二次追上乙。则甲出发后走了多少米第一次到达乙的出发点?
160
200
240
280
某工厂先从边长为1米的正方形铁皮切割掉一个半径1米、圆心角为直角的扇形,再用剩余材料切割正方形。为充分利用原材料,希望所得正方形越大越好。若不考虑切割损耗,问所切最大的正方形边长约为多少厘米?
22.6
25.6
27.6
31.6
悟空与二郎神在离地面1米的空中决斗,两人相距2米,悟空想用分身直接偷袭二郎神,为了不引起对方的警觉,分身必须在地面反弹一次再进行攻击,则分身到达二郎神的位置所走的最短距离为:
![]() 米
米
![]() 米
米
![]() 米
米
![]() 米
米
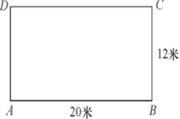
如图,在长方形跑道上,甲、乙两人分别从A、C处同时出发,按顺时针方向沿跑道匀速奔跑,已知甲、乙两人的速度分别是5米/秒、4.5米/秒。则当甲第一次追上乙时,甲沿长方形跑道跑过的圈数是:
4
4.5
5
5.5
甲、乙两人从环形跑道的A点同时出发背向而行,6分钟后两人第一次相遇,相遇后两人的速度各增加10米每分钟,5分钟后两人第二次相遇。问环形跑道的长度为多少米?
600
500
400
300
将一块三角形绿地沿一条直线分成两个区域,一为三角形,一为梯形,已知分出的三角行区域的面积为1.2亩,梯形区域的上、下底边分别为80米、240米,问分出的梯形区域的面积为多少亩:
9.6
11.2
10.8
12.0
一个正六边形跑道,每边长为100米,甲、乙两人分别从两个相对的顶点同时出发,沿跑道相向匀速前进。第一次相遇时甲比乙多跑了60米,问甲跑完三圈时,两人之间的直线距离是多少:
100米
150米
200米
300米