一些环保主义者是热爱旅游的人,所有的环保企业代表都支持减少风景区开发,所有热爱旅游的人都反对减少风景区开发。
由此可知:
所有环保主义者都反对减少风景区开发
所有的环保企业代表都不热爱旅游
一些热爱旅游的人支持加大风景区开发
一些环保主义者支持减少风景区开发
一条双向铁路上有11个车站,相邻两站都相距7千米。从早晨7点,有18列货车由第11站顺次发出,每隔5分钟发一列,都驶向第一站,速度都是每小时60千米;早晨8点,由第1站发一列客车,向第11站驶出,时速100千米,在到达终点前,货车与客车都不停靠任何一站。那么,在哪里客车能与3列货车先后相遇:
在第四、五站之间
在第五、六站之间
在第六、七站之间
在第七、八站之间
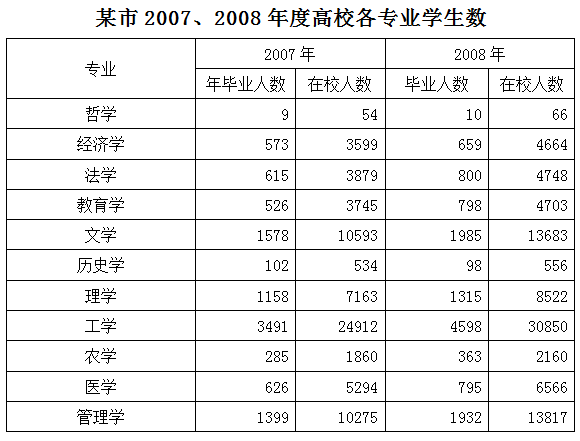
2007年的毕业生中,文学专业所占的比例大概是多少:
10%
12%
15%
18%
日常工作中,如果一件事发展得太过顺利,我们总会隐隐觉得有哪里不对,这样的直觉是有道理的。澳大利亚和法国的研究者们最近在某学术期刊上发表了一篇文章,说明了为什么当所有的证据都指向同一个结果时,它反而可能有问题。他们将此称之为“一致性悖论”。
研究者以证人指认犯人为例研究了一致性悖论,发现在辨认嫌疑人过程中,系统偏差可能来自多种心理偏差,如警方给证人展示照片的方式、证人自身的个人偏见等。而研究者发现,哪怕是细小的偏差都会对最终的整体结果产生极大影响。具体来讲,即使在1%的辨认过程中施加偏差,如暗示某人是犯人,最终当3个以上的证人意见一致时,他们的意见就不再可靠。有趣的是,如果_______,那么其他证人正确的概率反而会大大增加。
为什么会这样?可以用数学中的贝叶斯分析来说明。以扔硬币为例:如果我们有一枚硬币,扔到正面的概率为55%,而非普通硬币的50%,只要扔的次数足够多,就会发现正面向上多于反面向上的次数,进而发现这个硬币是有问题的。换句话说,当我们看到投掷结果中正面向上的次数显著多于反面向上时,就会意识到出问题的是硬币,而非概率定理。同样,根据概率定理,很多证人同时得到一致结论的可能性极低,所以更有可能的是系统出了差错。
在警方组织的嫌疑人指认中,指认同一个人有罪的证人数目越多,这个人真正有罪的概率就越大。然而,这只适用于没有任何系统偏差存在的理想情况。实际情况中,当指认同一个人为犯人的证人数目增加到一个值以后,该嫌疑人真正有罪的概率反而会下降,最终与随机指认毫无差别,且系统偏差越大,概率下降得越早。比方说,如果你让证人完成一项较为容易的任务,比如从一堆香蕉中找出一个苹果,所有人都几乎不会出错,多人结论一致的情况就可能出现,而指认犯人要比在一堆香蕉中找到苹果复杂得多。模拟显示,如果_______,他们认错人的概率会高达48%,在这种情况下,许多证人同时指认一个人为犯人的概率就相当低了;但如果_______,他们认错人的概率会大大降低,多个证人结论一致的情况出现的可能性也会提高。
在法律领域之外,一致性悖论还有很多用武之地,一个重要的应用就是加密技术。数据加密通常通过确认一个很大的数字是否为质数来进行,这个判断过程的错误率要达到非常低才行:低于2的负128次方才可以接受。在这一过程中,可能出现的系统差错就是计算机故障。大多数人都不会想到宇宙射线会导致电脑将一个合数误认为质数,毕竟这件事发生的概率只有10的负13次方——但要注意,这个概率要大于我们所要求的误差(2的负128次方),所以这类误差主导了整个过程的安全性。正因于此,加密协议所宣称的安全程度越高,实际的过程就越容易受计算机故障影响。
一致性悖论虽然听起来违背直觉,但研究者解释,一旦我们了解了足够的信息,就能理解它了。
如果要论证在指证嫌疑人的过程中不存在一致性悖论,则需要补充下列哪一组证明:
①所有证人都保持客观公正的态度
②所有证人都在犯罪现场看到了嫌疑人
③该名嫌疑犯在犯罪发生时的确在场
④该名嫌疑犯曾经犯过同样的罪行
⑤所有照片都体现出了嫌疑犯独有的外貌特征
⑥警察以同样方式对所有证人展示照片
①②⑥
①④⑤
②③⑤
③④⑥
有7名到大美公司应聘的人员:甲、乙、丙、丁、戊、己和庚,他们被安排在同一天的不同时段进行面试。每个人进行面试的时段各不相同,而且每人只进行一次面试。所有应聘人员不是硕士,就是博士。还知道如下条件:
(1)不存在面试顺序相邻两人都是硕士的情况;
(2)己的面试先于乙和丁;在己之前进行面试的人中恰好有两名硕士;
(3)甲是第6个进行面试的;
(4)庚的面试在丙之前进行。
据此可以得出,以下哪两人的面试不可能相邻?
戊和己
戊和丙
己和乙
己和庚
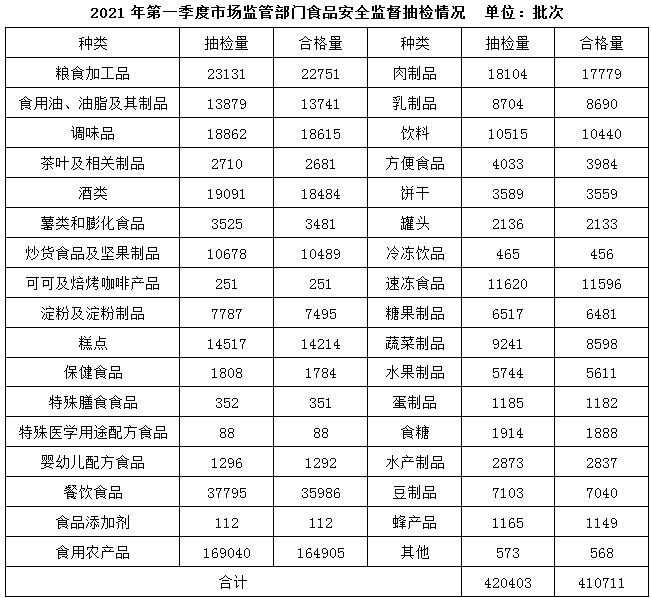
表中所列食品类别中,2021年第一季度所有抽检样本全部合格的有几类?
2
3
4
5
某省城镇就业人员增长明显快于乡村。2007年全省城镇就业人员比1978年增长2091.4万人,增加3.4倍,年均增长6% ;所占比重达到43.5% ,上升23.8个百分点。全省乡村就业人员比1978年增加1020.2万人,增长40.8% ,年均增长1.2% ;所占比重为56.5% ,下降23.8个百分点。
非农产业成为就业的主导产业。2007年全省第三产业就业人员比1978年增加1574万人,增加2.9倍,年均增长7.1% ,所占比重达到了34% ,上升16.6个百分点,成为拉动就业增长的主要力量。与1978年相比,第一产业就业人员减少85.7万人,所占比重下降了37.0个百分点;第二产业就业人员增加1623.3万人,所占比重上升20.4个百分点。
非公有经济的就业比例迅速上升,1978年全省个体经济就业人员仅有2353人。2007年个体工商户就业人员达到了397.8万人,所占比重为6.4% ;私营企业就业人员达到522.7万人 ,比重为8.4% ;港澳台企业就业人员27.4万人,比重为0.4% ;外商投资企业就业人员108.3万人,比重1.7% 。
1978年,该省乡村就业人员所占比例为城镇就业人员的多少倍:
1.3
4.1
8.7
无法计算
孩子的经济成本由孩子出生前后费用支出构成。
孩子出生前的有关支出,即从怀孕至孩子出生这段时期与孩子相关的费用估计平均为2685.36元。其中在孩子出生前费用比中名列前三名的是怀孕期间的营养费(38.58%)、住院接生费(26.91%)和婴儿用品预购费(23.46%)。胎教支出相对有限,只占6.03%。处于各项支出的最后一位。统计结果表明,男孩的妊娠分娩费用(3216元)要比女孩的费用(2109元)高,高出的部分主要体现在额外营养费、雇工照顾费和婴儿用品预购费上的性别差别,生男孩的母亲要比生女孩的母亲多进补289元,高出37.1%;生女孩的家庭几乎不请雇工帮忙,比生男孩的家庭少支出195元的雇工照顾费;男孩的婴儿用品预购费比女孩高出631元,是女孩的3.5倍。
孩子出生后,抚养其0—16周岁的费用为118934.45元。食品费用支出最多,为52314.68元;教育费用次之,为23615.31元;然后依次是家庭生活服务费(12651.68元)、衣着费用(11683.94元)、零花和压岁钱的支出(9876.85元)、文化娱乐活动的支出(8431.25元)、健康保险费(5216.34元)、日用品支出(4562.31元)和医疗保健费(3984.62元)。
从孩子出生后的抚养费用构成来看,食品费用支出占抚养费的比例约是文化娱乐活动支出所占比例的:
5.3倍
4.7倍
7.3倍
6.2倍
某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人。为了解该单位职工的健康情况,计划用等比例分层抽样的方法从中抽取样本。若样本中的青年职工为7人,则会抽取职工总人数为:
7
15
25
35
当人们陷于心理压力时,牺牲、自怜、延迟以及倦怠的感觉会产生,他会发现再去奋斗变得非常困难,而且会把所有的事情一拖再拖。处理未知的事物变成是一个非常困难的考验,而且要去了解未来,也会造成相当的困扰;最好的方法似乎是让所有事情都维持现状。
这段话主要想表达的意思是:
压力发生在心理上会引发许多问题
人们因为发现奋斗非常困难,所以把所有事情一拖再拖
维持现状是解决心理压力的最好办法
现代社会必然会导致出很多心理问题