某单位有南、北两个绿化区,拟在其中种植一些果树。员工们推荐了4种果树备选:杏树、桃树、苹果、柿子。根据实际情况,还需满足以下3项种植要求:
(1)每区种植3种果树;
(2)至少要在一个绿化区同时种植杏树和苹果;
(3)种植桃树的绿化区也要种植柿子。
下列选项中,一定错误的是:
两个区都种有桃树
两个区都种有苹果
只有一个区种有杏树
只有一个区种有苹果
钱学森曾提出一个问题,后来被称为“钱学森之问”:为什么我们的学校总是培养不出杰出人才?虽然他当时只是针对科学研究而言,但这个问题可以推广到很多领域。比“钱学森之问”更为具体的问题是:相对于我们的人口规模,相对于我们的经济总量,相对于我们的教育投入,从我们的教育体制中走出来的具有创造力的人才,为什么这么少?
创造性思维首先来源于知识,这似乎没有争议。不过,对知识的界定需要更多思考。我们说的知识通常指学科和领域的专业知识。但是,知识也应该包括跨学科知识、跨领域知识、跨界知识。创造力多产生于学科交叉和融合。所以对“钱学森之问”的第一个回答是:学生的知识结构有问题,我们的学生过多局限于专业知识,而缺乏跨学科、跨领域、跨界知识,而这些往往是具有创造力的人才的特征。
创造性思维的第二个来源是好奇心和想象力。爱因斯坦说过,“________________”。他还说过,“________________”,在我们以知识为中心的教育中,这些知识以外的因素通常不受重视。知识与受教育年限的关系比较简单,通常随着受教育年限的增多而增多,但好奇心和想象力与受教育年限的关系则更取决于教育环境和教育方法。儿童时期的好奇心和想象力特别强,但是随着受教育的增多,好奇心和想象力很有可能会递减。这是因为,知识体系都是有框架、有假定的,难怪爱因斯坦感叹过,“________________”。如果这些分析是对的,那么对“钱学森之问”的第二个回答是:不是我们的学校培养不出杰出人才,而是我们的学校在增加学生知识的同时,有意无意地限制了创造性人才的必要因素——好奇心和想象力的发展。
创造性思维的第三个来源与价值取向有关,也就是与追求创新的动机和动力有关。创新的动机有三个层次,分别代表了三种价值取向:短期功利主义、长期功利主义和内在价值的非功利主义,每一个后者都比前者有更高的追求。对短期功利主义者而言,创新能够在短期带来奖励。对长期功利主义者而言,创新需要经过长期努力才能见到成效。而对内在价值的非功利主义者而言,创新源于一种内在动力,源自一种永不满足于现状的渴望,一种发自内心、不可抑制的激情,而不是为了个人的回报和社会的奖赏。现实情况是,具备第一类动机的人很多,具备第二类动机的人也有,但具备第三类动机的人就寥寥无几了。然而,科学和社会的殿堂中如果没有他们,就不成其为殿堂。所以,对“钱学森之问”的第三个回答是:我们之所以缺乏创造性人才,除了知识结构问题和缺乏好奇心和想象力之外,就是在价值取向上太“立竿见影”急于求成的心态,这样的价值观很难出现颠覆性创新、革命性创新。
将下列三个句子依次填入文中划横线处,正确的顺序是:
①我没有特殊的天赋,我只是极度地好奇
②好奇心能够在正规教育中幸存下来,简直就是一个奇迹
③想象力比知识更重要。因为知识只是局限于我们已知的一切,而想象力将包括整个世界中那些未知的一切
①②③
①③②
②③①
③②①
张飞和李柏今年都报考了MBA,关于他们的考试有如下四个断言:
(1)他们两人至少有一个考上;
(2)张飞并不必然考上;
(3)李柏确实考上了;
(4)并非张飞可能没考上。
最后录取结果表明:这四个断言中有两个是真的,两个是假的。
下面哪一个结果可以从上述条件推出:
张飞考上了,李柏没考上
张飞和李柏都考上了
张飞和李柏都没考上
李柏考上了,张飞没考上
在下图小空格中已填上了1及7两个自然数,如果其他空格也填上相应不同的数,使得任意一个横行、任意一个纵列以及任意一条对角线上的3个数之和都等于111。请问,位于中间的小正方形里应填的数是:
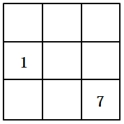
61
53
41
37
山东手造精品众多,某展览会有叶雕、皮影、风筝、麦秸画、柳编、葫芦画、锡雕、鲁班枕8个展厅。因时间原因,一名参观者决定从8个展厅中随机选取3个进行参观。问叶雕和皮影展厅至少一个被选中的概率是多少?
![]()
![]()
![]()
![]()
初步核算,2012年我国国内生产总值519322亿元,扣除价格因素,比上年增长7.8%。其中,第一产业增加值52377亿元,增长4.5%;第二产业增加值235319亿元,增长8.1%;第三产业增加值231626亿元,增长8.1%,2003-2011年我国国内生产总值、人均国内生产总值及其增长数据见图1和图2。
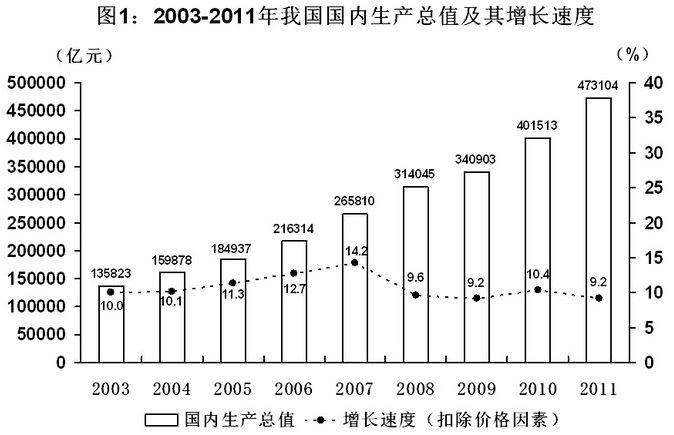
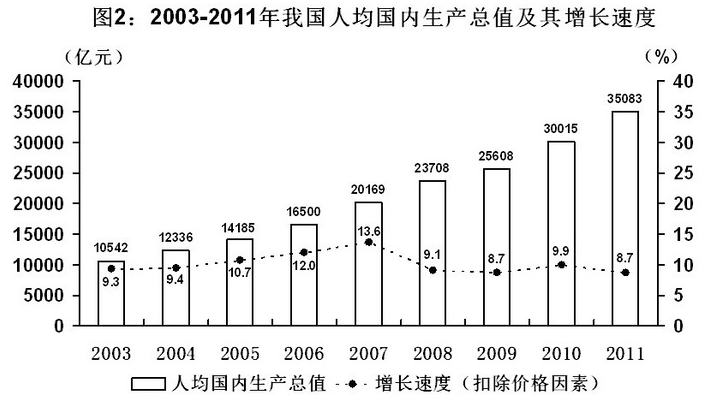
2004-2012年九年,我国国内生产总值年增加量最少的年份是:
2004年
2009年
2011年
2012年
教师从某班级学号为01~07的7名学生中随机抽出3名做值日,则这3名学生学号恰好为三个相邻自然数的概率为:
七分之一
六分之一
五分之一
四分之一
小芳与小莲是一对好朋友,大刚与大勇也是,但这四人彼此间却不太熟悉。在一次机关联谊会上,小芳、小莲和大刚、大勇相遇,
小芳能叫出大刚的名字,但大刚却叫不出小芳的名字。
凡能叫出大刚名字的人都能叫出大刚朋友的名字,
凡叫不出小芳名字的人都叫不出小芳朋友的名字。
根据以上信息,可以得出以下哪项:
小莲能叫出大刚的名字
大刚能叫出小莲的名字
小芳能叫出大勇的名字
大勇能叫出小芳的名字
由1~9中的数字组成一个3位数,有数字重复的情形有多少种:
220
255
280
225
有20位运动员参加长跑,他们的参赛号码分别是1,2,3,…,20,至少要从中选出多少个参赛号码,才能保证至少有两个号码的差是13的倍数:
12
15
14
13