四个人在议论一位作家的年龄。
甲说:“她不会超过35岁。”
乙说:“她不超过40岁。”
丙说:“她的岁数在50以下。”
丁说:“她绝对在40岁以上。”
实际上只有一个人说对了。
那么下列说法正确的是:
甲说的对
她的年龄在45~50岁之间
她的年龄在50岁以下
丁说的对
中世纪数学家比萨的莱奥纳多发现了斐波那契数列,它是这样一组数列:1、1、2、3、5……即后一数字为前面两个数字之和。那么,数列和树木的成长有什么关联呢?由于新生的枝条,往往需要一段“休息”时间,供自身生长,而后才能萌发新枝。所以,一株树苗在一段间隔,例如一年,以后长出一条新枝;第二年新枝“休息”,老枝依旧萌发;此后,老枝与“休息”过一年的枝同时萌发,当年生的新枝则次年“休息”。这样,一株树木各个年份的枝桠数,便构成斐波那契数列。
这段文字意在说明:
斐波那契数列表现为树木的年轮增长
斐波那契数列在自然界中无处不在
斐波那契数列在自然中的应用
斐波那契数列表明植物在大自然中长期适应和进化
某超市从前到后整齐排列着7排货架,放置着文具、零食、调料、日用品、酒、粮油和饮料7类商品,每类商品占据一排。已知:
(1)酒类排在调料类之前;
(2)文具类和调料类中间隔着3排;
(3)粮油类在零食类之后,中间隔着2排;
(4)日用品类紧挨在文具类前一排或者后一排。
零食类和文具类中间最多可能隔几排?
2排
3排
4排
5排
有两位年轻人张某和李某在一起喝茶聊天,张某问李某:“在立业和安家这两大任务面前,你是打算先立业还是先安家呢?”
张某提问的假设前提是:
立业是安家的充分条件
立业是安家的必要条件
立业和安家很难同时进行
立业和安家互不相关
国家统计局采用定基指数方法,以2014年为100,根据第四次全国经济普查数据修订结果以及部分指标最新数据,将5个分类指标的权重均设定为0.2,对2015~2019年我国经济发展新动能总指数进行测算,结果见下表。
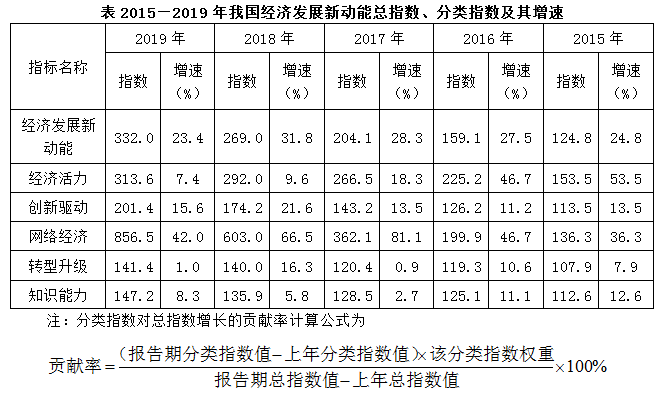
2015~2019年我国经济发展新动能总指数值比上年增加最多的年份是:
2016年
2017年
2018年
2019年
一块三角形农田ABC(如下图所示)被DE、EF两条道路分成三块。已知BD=2AD,CE=2AE,CF=2BF,则三角形ADE、三角形CEF和四边形BDEF的面积之比为:
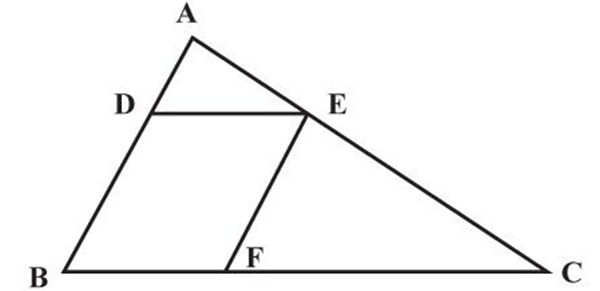
1:3:3
1:3:4
1:4:4
1:4:5
下面四个齿轮中,哪个每分钟转的次数最多:
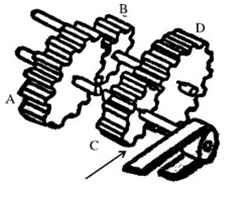
如图所示
如图所示
如图所示
如图所示
某公司举行假面舞会。张先生与张女士头戴不同颜色的面具相遇。
“我是一位先生。”戴红色面具的那位说。
“我是一位女士。”戴黄色面具的那位说。
说完后,两人都笑了。因为他们两人中至少有一个人在说谎。
据此,可以推断出下列哪项判断为真:
张先生说真话,他戴红色面具
张先生说假话,他戴黄色面具
张女士说真话,她戴红色面具
张女士说假话,她戴黄色面具
小张每连续工作5天后休息3天,小周每连续工作7天后休息5天。假如3月1日两人都休息,3月2日两人都上班,问三月份有多少天两人都得上班:
12
14
16
18
甲、乙、丙、丁、戊、己六位运动员的跳高纪录有如下比较:
(1)乙的成绩比丙好,但不如甲;
(2)丁的成绩不如甲和丙;
(3)戊的成绩好于丁和己,但不如甲和丙。
由此,可以确定:
丁的成绩好于己
己的成绩好于丁
戊的成绩好于乙
乙的成绩好于戊