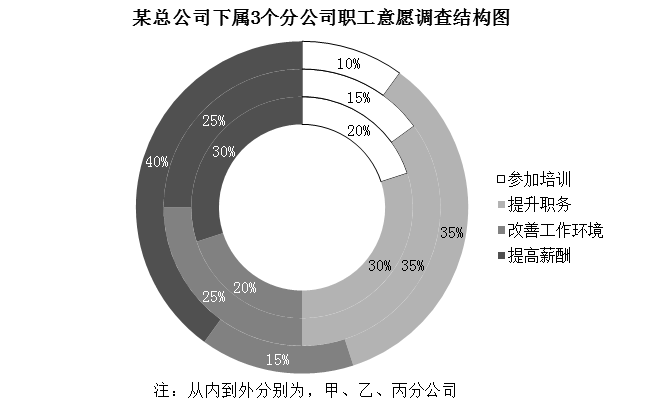
假设甲、乙、丙3个分公司的职工人数相同,总公司某年度计划对3个分公司中有意愿提升职务的职工进行职务提升,晋升比例为每5位有意愿的职工中提升1位,那么:
甲分公司获得职务提升的职工人数不一定比乙、丙的少
乙分公司获得职务提升的职工人数不可能多于甲分公司
甲、乙、丙3个分公司获得职务提升的职工人数之和将超过甲分公司职工总人数
乙、丙分公司获得职务提升的职工人数不一定相同
甲、乙和丙,一位是山东人,一位是河南人,一位是湖北人。现在只知道:丙比湖北人年龄大,甲和河南人不同岁,河南人比乙年龄小。
由此可以推知:
甲不是湖北人
河南人比甲年龄小
河南人比山东人年龄大
湖北人年龄最小
某小微企业接到三个相同的订单,赵、钱、孙、李四位师傅单独完成一个,分别需20小时、20小时、15小时和12小时。现钱、孙、李各负责一个订单,赵根据需要协助他们完成任务。若要三个订单同时完工且用时最短,则赵协助钱的时间是:
8小时
7小时
6小时
9小时
在数列![]() (n=1,2,…,)中,
(n=1,2,…,)中,![]() =1959,
=1959,![]() =1995,且从第三项起,每项是它前两项平均数的整数部分,则
=1995,且从第三项起,每项是它前两项平均数的整数部分,则![]()
![]() =
=
1980
1981
1983
1982
三个学生共解出30道数学题,每人都解出了其中的12道,且每道题都有人解出。只有一人解出的题叫做难题,只有两个人解出的题叫做中等题,三人都解出的题叫做容易题。在这30道题中,难题、中等题、容易题均有,且题数各不相等,则难题的题数是:
14
15
22
25
设一边长为3的正三角形S1,将S1的每条边三等分,在中间的线段上向形外作正三角形,去掉中间的线段后所得到的图形记为S2;同理将S2的每条边三等分,并重复上述过程所得到的图形记作S3。那么S3与S1的周长之比为多少?
64∶27
16∶9
4∶3
4∶3
十八世纪一位德国数学家在写给著名数学家欧拉的一封信中,提出了一个猜想。该猜想可以表述为:(一)任何不小于6的偶数,都是两个奇素数之和;(二)任何不小于9的奇数,都是三个奇素数之和。我国著名数学家陈景润在证明这一猜想中作出了重大贡献,这个猜想是:
莫德尔猜想
哥德巴赫猜想
康威一诺顿猜想
四色猜想
下图为给定的多面体,将其沿a、b、c三个顶点所在的平面切开,其截面是?【2025联考/甘肃074】
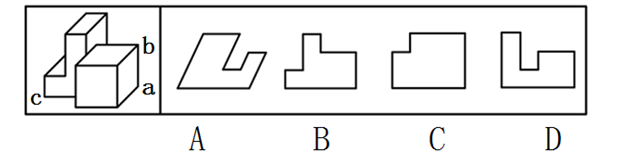
如图所示
如图所示
如图所示
如图所示


当年非蓝天日数排名前10位的城市中,未能将非蓝天日数的同比增速控制在10%以下的城市有几个:
4
5
6
7
汽车厂甲、乙、丙三个机器人承担拧螺丝任务,程序设定甲先开始,3分钟后乙开始,再3分钟后丙开始。当乙工作12分钟时,所拧的螺丝数与甲拧的螺丝数相同,丙工作20分钟时,所拧的螺丝数与甲拧的螺丝数相同,则丙的工作效率是乙的:
1.04倍
1倍
0.9倍
0.8倍