一位教师表达了她对电子游戏给中小学生带来危害的焦虑之情。她认为电子游戏就像一头怪兽,贪婪、无情地剥夺了中小学生的学习和与社会交流的时间。
以下哪项不能成为支持以上观点的理由:
中小学生玩电子游戏上课时无精打采
中小学生玩电子游戏不愿与家长交谈
中小学生玩电子游戏花费了家里的资金
中小学生玩电子游戏作业错误明显增多
美国的一位动物学家在黑猩猩的笼子前放了一面大镜子,观察他们的反应。它们能够从镜子中认出自己,经常久久地对着镜子寻找自己身上平时看不到的部位。作为黑猩猩近亲的大猩猩却不具备这种能力。
由此可以推出:
黑猩猩在某些方面的能力高于大猩猩
黑猩猩和大猩猩虽然亲缘较近,但还是黑猩猩的智力更胜一筹
黑猩猩的这种能力和它所生活的环境有关
动物界还有其它动物具备这种能力
在所有电脑标志中,“@”是唯一入选纽约现代艺术博物馆建筑与设计收藏的标志。它也是网络世界最常用的符号。每个电子邮件都要用到它,在微博里通知他人,也要用到它。“@”在数字世界的使用最早是在1971年。美国技术研究公司BBN的一位程序员雷蒙德·汤姆林森当时正负责开发一个程序让计算机用户能够连接到阿帕网。他决定在电脑网络的地址中间插入这个符号,来区分“用户”和“终端”,这个做法后来被广泛采用,成了今天电子邮件地址的标准写法。因此,雷蒙德·汤姆林森也被称为“电子邮件之父”。
这段文字旨在说明:
“@”被作为电脑符号的由来
“@”在网络中是最常用的符号
“@”入选现代艺术标志的原因
将“@”作为电脑符号的第一人
12,19,29,47,78,127,( )
199
235
145
239
7,13,19,29,( ),53
30
39
44
49
文化广场举行放风筝比赛,老年组老王、老侯、老黄三位选手同场竞技,评委测量各人放出的风筝线长分别为60米、50米、40米,风筝线与地平面所成的角分别为π/6、π/4、π/3,假设风筝线看作是拉直的,则三位选手放风筝最高的是:
老黄
老侯
老王
不能确定
S市统计局在该市范围内,抽取3000名18~70周岁且在2013年有过网购经历的居民,以入户方式进行问卷调查。
调查数据显示,受访者2013年人均网购次数为19.4次。从分组情况看,有三类人群使用网购相对频繁:一是年轻群体。35岁以下的受访者人均网购次数为25.5次;二是较高学历的群体,文化程度为大学本科及以上学历和大专学历的受访者人均网购次数分别是27.3次和21.8次;三是中高收入群体,个人月收入为10000元以上和5000~10000元的受访者人均网购次数分别是31.0次和26.0次。此外,女性受访者人均网购次数为21.1次,比男性受访者高出3.8次。2013年该市网购10类主要商品和服务的受访者占比情况如下图。
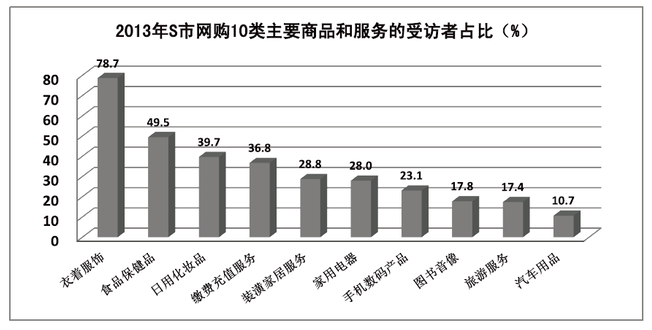
受访者中,在2013年网购了缴费充值服务的人数为网购图书音像人数的:
1.6倍
2.1倍
2.5倍
3.0倍
日前,我认真拜读了一位老领导的回忆录,为他认真做事的态度而深深感动。他曾是一位县委书记,后来担任了市长,可他的第一份工作却是生产队的记分员。所谓记分员,就是负责记录队员每日工作情况的农民。这个在旁人看来“不起眼”的工作,他却十分喜爱,干得起劲。记分,一丝不苟,不偏不漏,客观公正,做到了让队长满意、让群众满意。因此,6年后被提拔为公社干部。他在回忆录中写道:基层6年,为以后40多年的工作打下了坚实基础。
这段话对做好机关工作最主要的启示是:
要尽量把每一件事都做好
要以客观公正为准则做事
要认真做好“不起眼”的小事
要从最基层的工作做起
素数是指只含有两个因子的自然数(即只能被自身和1整除),孪生素数是指两个相差为2的素数。比如,3和5,17和19等。所谓的孪生素数猜想,是由希腊数学家欧几里得提出的,意思是存在着无穷对孪生素数。该论题一直未得到证明。近期,美国一位华人讲师的最新研究表明,虽然还无法证明存在无穷多个之差为2的素数对,但存在无数多个之差小于7000万的素数对。有关方面认为,如果这个结果成立,那么将是数论发展的一项重大突破。
以下哪项如果为真,最能支持有关方面的观点:
7000万这个数字很大,离孪生素数猜想给出的2还有很大距离
这是第一次有人正式证明存在无穷多组间距小于定值的素数对
关于孪生素数猜想的证明需要一个漫长的、逐步推进的过程
这位华人讲师长期从事数学领域的相关教学和科研工作
某学校举行迎新篝火晚会,100名新生随机围坐在篝火四周,其中,小张与小李是同桌,他俩坐在一起的概率为:
![]()
![]()
![]()
![]()