[单选题]

举办一次菊花展，将42盆某品种的菊花摆放成若干排。若从第二排开始，每一排的菊花盆数都比前一排多1盆，则摆放的方案有：

A . 2种
B . 3种
C . 4种
D . 5种

参考答案： B

参考解析：

①设未知数：
设摆放方案中共有n排，第一排有a盆菊花（a为正整数，n≥1）。
由于从第二排起每排比前一排多1盆，这是一个首项为a、公差为1的等差数列，总盆数为42盆。
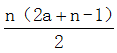根据等差数列求和公式：总盆数S=×[2a+(n−1)]，即42=，化简得n(2a+n−1)=84。

②明确约束条件：
分析等式n(2a+n−1)=84，其中2a+n−1必为正整数，且2a=−n+1。由于a是正整数，因此−n+1必须是正偶数，即−n+1>0且为偶数。
进一步推导：>n−1，即n(n−1)<84。同时，n是84的正因数（因n需整除84）。

③筛选有效方案：
列出84的所有正因数，并筛选符合条件的n：
84的因数有1、2、3、4、6、7、12、14、21、28、42、84。
当n=1时：2a=84−1+1=84，a=42（符合）。
当n=2时：2a=42−2+1=41（41不是偶数，排除）。
当n=3时：2a=28−3+1=26，a=13（符合）。
当n=4时：2a=21−4+1=18，a=9（符合）。
当n=6时：2a=14−6+1=9（9不是偶数，排除）。
当n=7时：2a=12−7+1=6，a=3（符合）。
n≥12时：n(n−1)≥12×11=132>84，不符合条件，排除。
符合条件的n有1、3、4、7，共4种方案。

故本题选B。
【2025-江苏B-059】

视频解析：